(研)现代运动控制策略-孙丹
- 跟其他电机控制or建模笔记中保持一致,正体的\(\text p\)表示海氏算子,斜体的\(p\)表示极对数。
矢量控制
- 基本概念:矢量控制也称为磁场定向控制(Field-Oriented Control, FOC),是将异步电动机通过坐标变换转换为同步旋转的直流电动机,将定子电流矢量分解成互相解耦的励磁电流标量和转矩电流标量,从而使异步电动机模拟直流电动机的工作方式对转矩和转速进行动态控制。
- 解耦方向:
- 异步电机:M-T坐标系的M轴选定在异步电机转子全磁通方向
- 电励磁同步电机:M-T坐标系的M轴选定在气隙磁通方向
- 永磁同步电机:d-q坐标系的d轴选定在永磁同步电机转子永磁磁通方向(其实也就是气隙磁通,一样的)
基频以下电压补偿控制
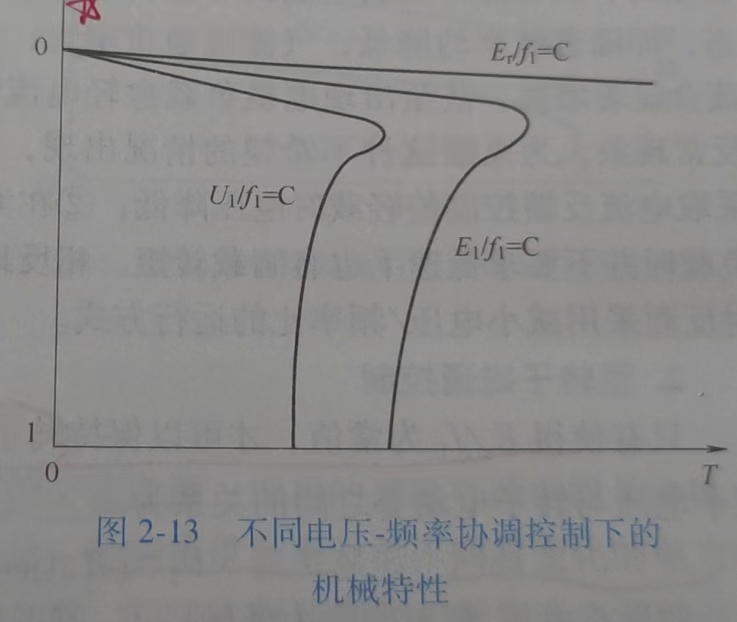
| 恒气隙电势频比 \(E_1/f_1\) | 恒电压频比 \(U_1/f_1\) | 恒转子磁通(转子电势) \(E_r/f_1\) | |
|---|---|---|---|
| 特点 | 气隙磁通 \(\phi_m\) 恒定 需要补偿定子阻抗上的压降 n-T 曲线纯向下平移 低频下 \(T_{st}\) 大,\(I_{st}\) 小 临界转差、转矩更硬,机械特性好 | 类似前一个,但控制更方便 最大转矩 \(T_{st}\) 随频率降低而减小 | 机械特性 n-T 为直线 不同同步速下,为一簇平行线 工作特性好,由高性能电机实现 |
坐标变换
坐标变换仍然可以参考电机建模:电机系统建模与分析 | Paradox's Website (zju-paradox.top),电机建模里面是恒幅值变换(前面有一章是恒功率变化,那里需要把系数 \(\frac23\) 换成 \(\sqrt{\frac23}\))。关于 \((\alpha-\beta-0)\) 到 \((d-q-0)\) 的坐标变换方式在文章里已经写的很明白了,这里不再赘述。
在画控制框图的时候,只需要简化成一个黑盒,需要对应的角度\(\theta\)(如异步电机就是转子磁场角度)
- 声明:在《电机控制(年珩)》的书以及孙丹的PPT上,后续有些地方省略(漏写)了变换系数\(\frac23\),所以前后会有公式不匹配的情况出现。学习的时候注意甄别,不过也不需要拘泥于具体公式,只要原理一致就行。
异步电机矢量控制
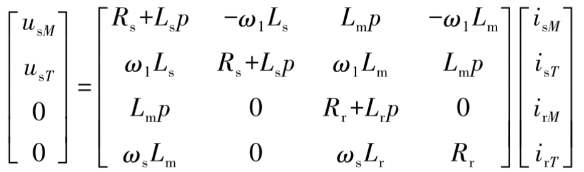
\[ T_e=\frac32p(\varPsi_Mi_T-\varPsi_Ti_M)=\frac32p\frac{L_m}{L_{22}'}\varPsi_{rM}i_{sT} \]
这条电磁转矩的公式非常重要,这条公式表明,异步电机电磁转矩直接由M轴转子磁通和T轴定子电流决定。
那么,转子磁链如何计算呢?公示如下:
\[ \varPsi_{rM}=\frac{L_m}{1+T_2\text p}i_{sM} \]
也就是说,转子磁链仅由定子电流励磁分量\(i_{sT}\)确定,这样电磁转矩可由定子电流的两个分量完全控制。当然,由于上述公式里的\(\text p\)是海氏算子,因此表明定子电流励磁分量对转子磁通的控制有延后,因此一般维持转子磁通不变,调节定子电流的转矩分量即可实现瞬态控制。
转子磁链定向
| 磁通检测—电压模型 | 磁通检测—电流模型 | 转差频率控制式 | |
|---|---|---|---|
| 输入 | 定子电压 \(u_{s\alpha\beta}\)、定子电流 \(i_{s\alpha\beta}\) | 定子电流 \(i_{s\alpha\beta}\)、电机转速 \(\omega_r\) | \(i_{sT}^*,\psi_{r^*},\omega\) |
| 过程 | \(\begin{gather*}\psi_{r\alpha}=\frac{L_r}{L_mp}[u_{s\alpha}-(R_s+\sigma L_sp)i_{s\alpha}]\\\psi_{r\beta}=\frac{L_r}{L_mp}[u_{s\beta}-(R_s+\sigma L_sp)i_{s\beta}] \end{gather*}\) | \(\begin{gather*}\psi_{r\alpha}=\frac{1}{\tau_rp}[L_mi_{s\alpha}-\omega \tau_r\psi_{r\beta}]\\\psi_{r\beta}=\frac{1}{\tau_rp}[L_mi_{s\beta}+\omega \tau_r\psi_{r\alpha}] \end{gather*}\) | \(\begin{gather*} \omega_s=\frac{L_mi_{sT}^*}{\tau_r\psi_r^*}\\=\frac{\tau_rp+1}{\tau_r}\frac{i_{sT}}{i_{sM}}\end{gather*}\) |
| 输出 | \(\begin{gather*}\psi_r=\sqrt{\psi_{r\alpha}^2+\psi_{r\beta}^2}\\\theta_M=\text{atg}(\psi_{r\beta}/\psi_{r\alpha}) \end{gather*}\) | \(\begin{gather*}\psi_r=\sqrt{\psi_{r\alpha}^2+\psi_{r\beta}^2}\\\theta_M=\text{atg}(\psi_{r\beta}/\psi_{r\alpha}) \end{gather*}\) | \(\theta_M=\int(\omega_s+\omega)\text dt\) |
| 优点 | 中高速准确 | 中低速准确 | 对电机参数变化不敏感 |
| 缺点 | 对电机参数变化敏感 | 对电机参数变化敏感 | 检测不了磁链幅值 |
注:\(\sigma\)为漏磁系数,计算方式为\(\sigma=1-\frac{L_m^2}{Ls-L_r}\)
注:前两种方法都可以得到磁链的幅值和角度,但转差频率控制式只能得到角度,这点在后面控制方式的选择上会有差异。
控制框图
电压源PWM
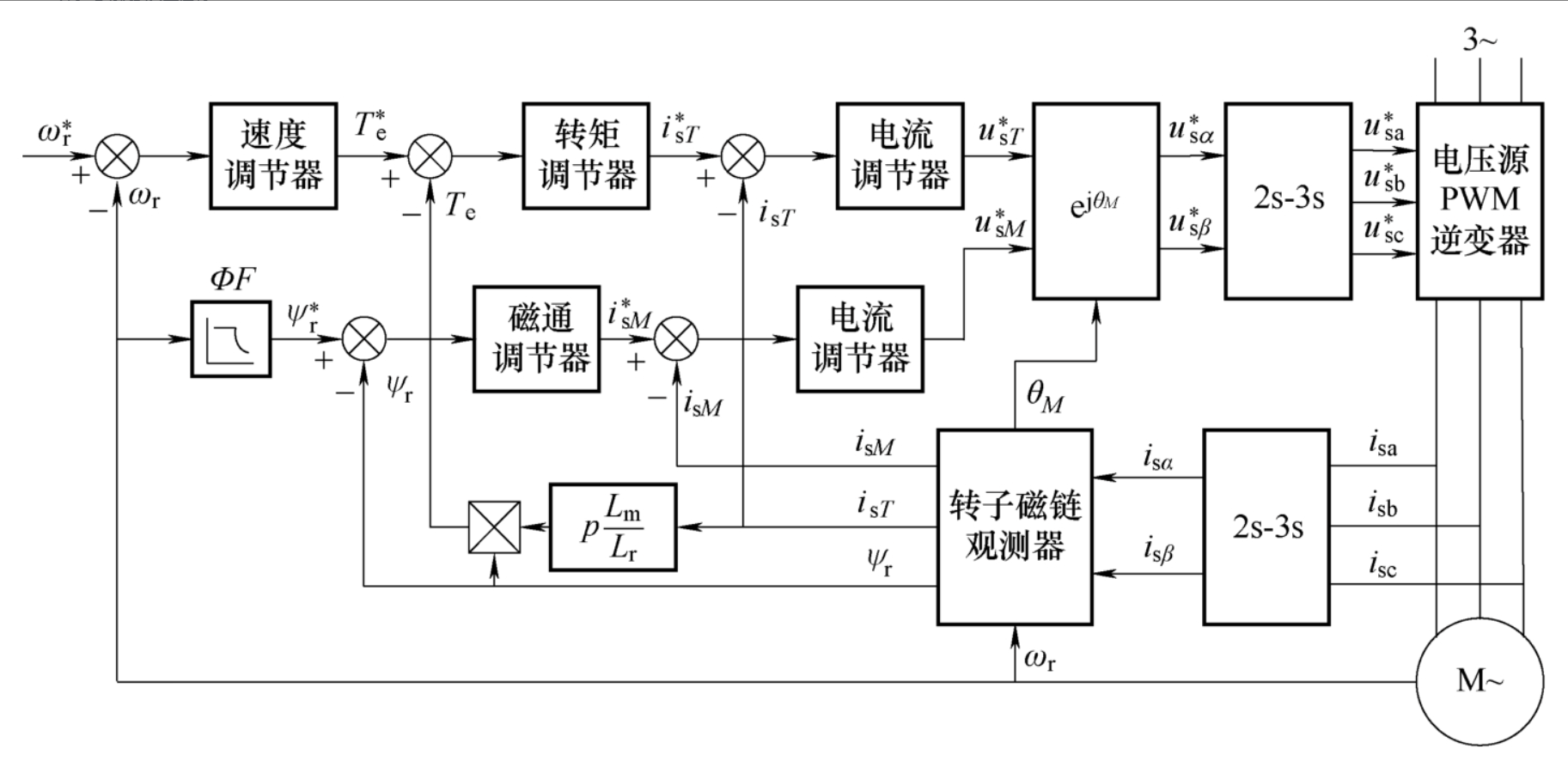
电流源PWM
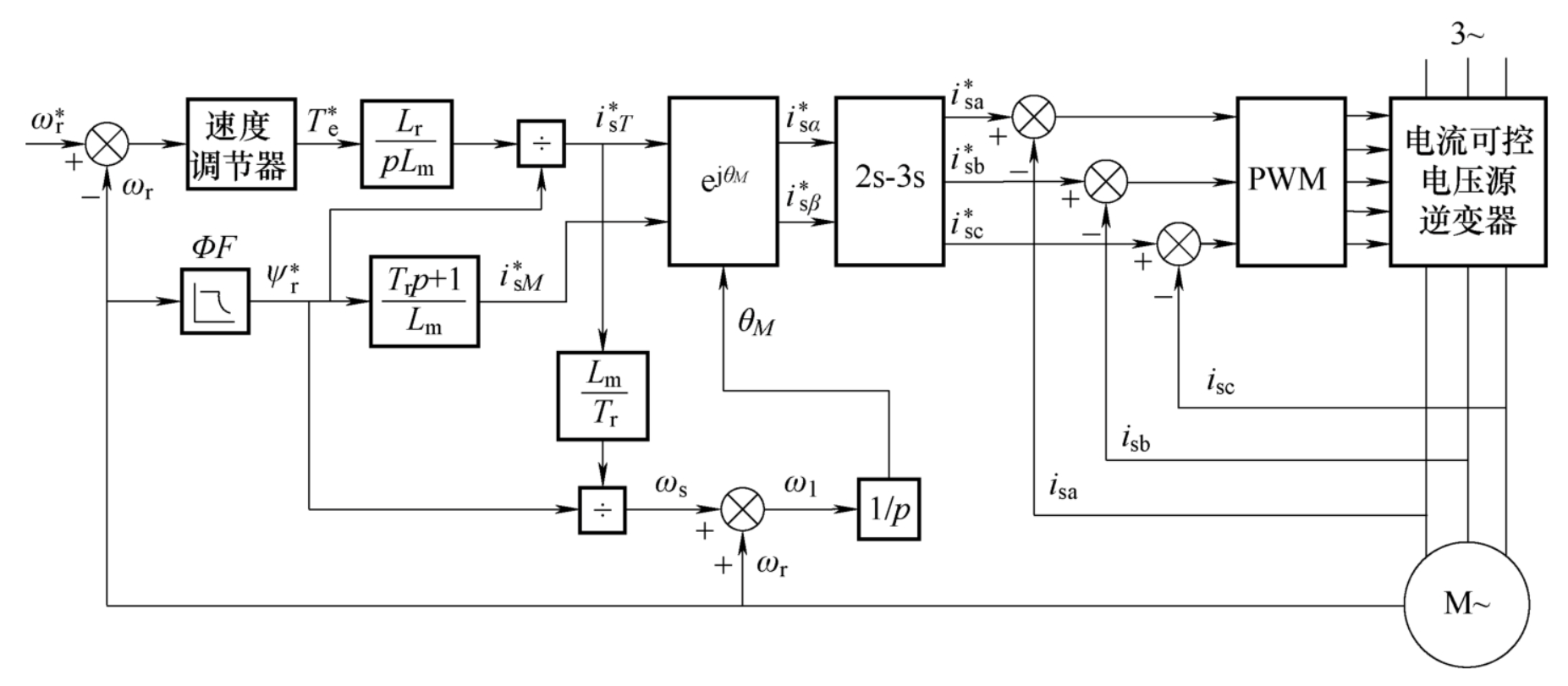
永磁同步电机矢量控制
如上文所述,永磁同步电机的坐标变换直接采用d-q轴方式:
\[ \begin{bmatrix} u_d\\u_q \end{bmatrix}=R_s\begin{bmatrix} i_d\\i_q \end{bmatrix}+\begin{bmatrix} L_d&0\\0&L_q \end{bmatrix}p\begin{bmatrix} i_d\\i_q \end{bmatrix}+\omega_r\begin{bmatrix} 0&-L_q\\L_d&0 \end{bmatrix}\begin{bmatrix} i_d\\i_q \end{bmatrix}+\omega_r\psi_f\begin{bmatrix} 0\\1 \end{bmatrix} \]
\[ \begin{bmatrix} \psi_d\\\psi_q \end{bmatrix}=\begin{bmatrix} L_d&0\\0&L_q \end{bmatrix}\begin{bmatrix} i_d\\i_q \end{bmatrix}+\begin{bmatrix} \psi_f\\0 \end{bmatrix} \]
\[ T_e=\frac32p(\psi_di_q-\psi_qi_d)=\frac32 p\left [\psi_fi_q+(L_d-L_q)i_di_q\right ] \]
- 将电磁转矩的前后两段分为励磁转矩和磁阻转矩:
- 对于内置式永磁同步电机,\(L_d < L_q\),直轴电枢反应助磁产生负的电磁功率,去磁却产生正的电磁功率,因此利用直轴电枢反应去磁作用可以提高电机的输出功率,并扩大调速范围
- 对于表贴式永磁同步电机,\(L_d = L_q\),只有励磁转矩。此时\(i_d=0\)控制等同于最大转矩/电流比控制
- 跟上文中比较有区别的是,永磁同步电机的气隙磁通就是永磁磁通\(\psi_f\),其幅值是一个已知的定值,角度就是转子运动角度\(\theta_r\),因此不需要观测器!
控制框图
\(i_d=0\)控制
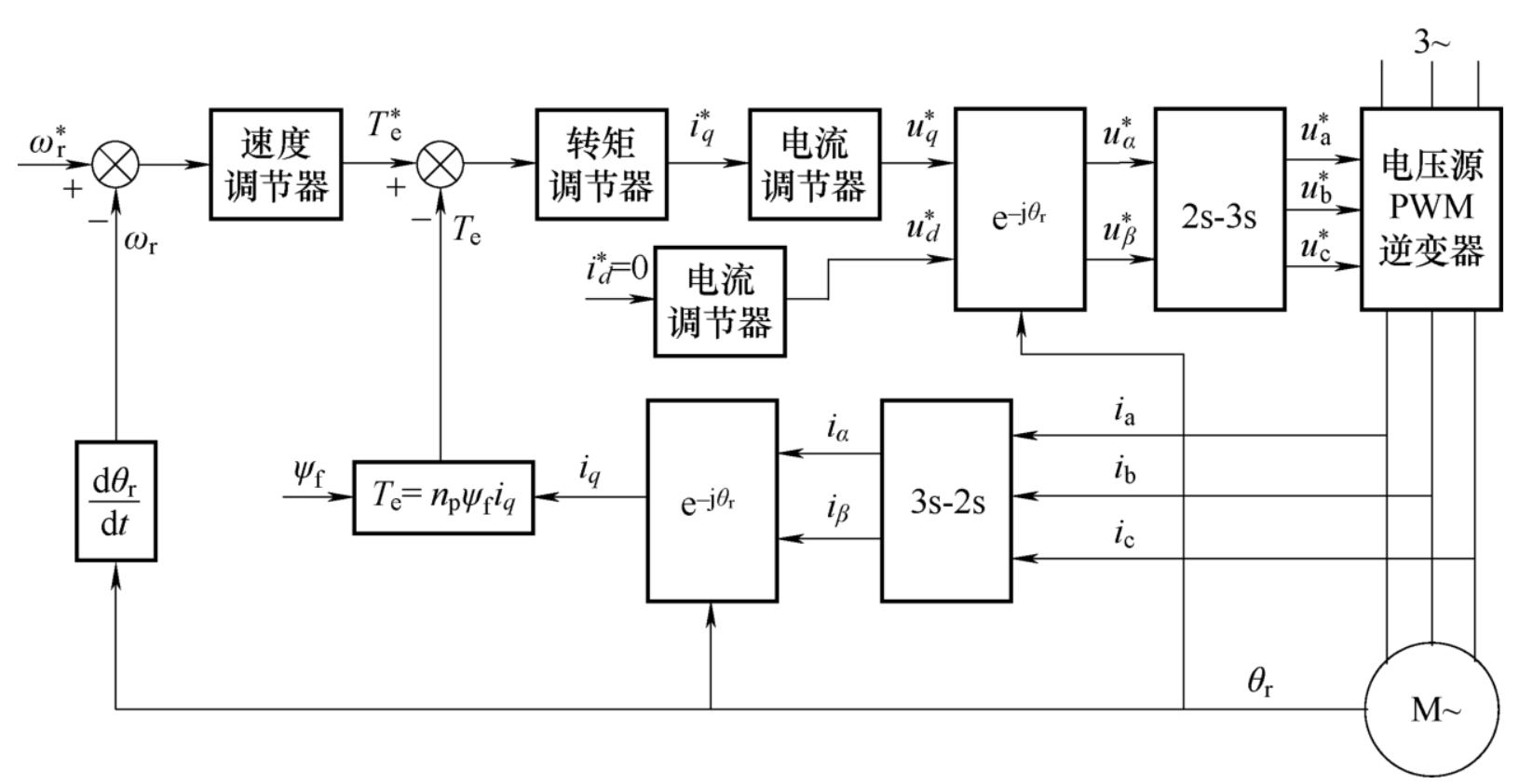
最大转矩电流比(MTPA)控制
根据标幺值计算\(T_e^*=i_d^*(1-i_q^*)\),在根据不同的方法算出所需的定子电流,进行电流环:
| 方法 | 公式法 | 查表法 | 探索法 | 高频信号注入法 |
|---|---|---|---|---|
| 实现方式 | \(T_e^*=\sqrt{i_d^*(i_d^*-1)^3}\) \(T_e^*=\frac{i_q^*}2(1+\sqrt{1+4i_q^{*2}})\) | 稳态且转矩给定时,以小步长改变电电流矢量角给定值,比较不同矢量角所对应电流检测值的大小,经过多次在线校正寻优 | 在控制侧基波信号上,叠加高频小信号,通过对注入的高频信号的处理,分析输出转矩的变化情况调整工作点 | |
| 优势 | 参数准确时计算准确迅速 | 在线运算少,硬件负担小 | 不依赖模型,鲁棒性高,无需复杂计算 | |
| 劣势 | 电机参数会受到温度、磁饱和等因素影响 | 离线测试工作量大,无法延拓 | 稳态时电流矢量角在极值处振荡;动态响应性能不佳 |
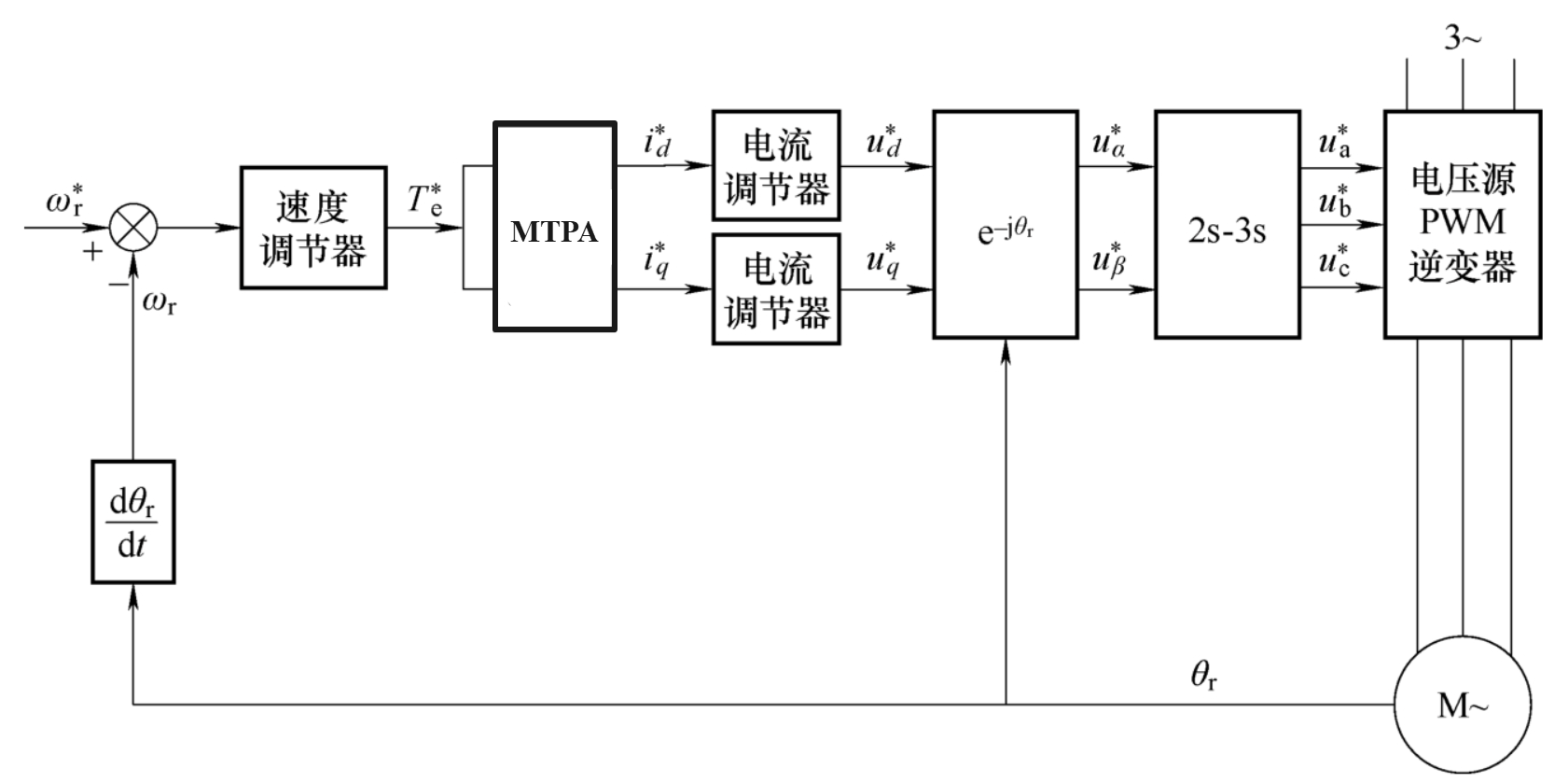
弱磁控制
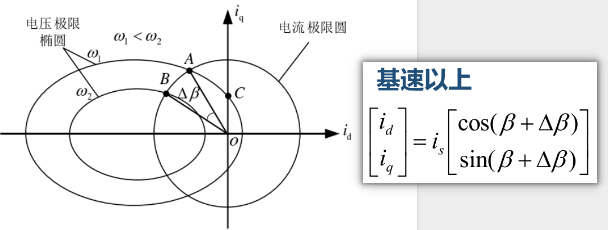
电压极限椭圆
受逆变器容量的限制,定子电流极限值\(|i_s|<|i_s|_{max}\),带入电压并忽略定子电阻压降,得:
\[ \begin{gather*} (e_0+x_di_d)^2+(\rho x_di_q)^2<|u_s|_{max}^2 \\ 或:\,\,(\psi_f+L_di_d)^2+(\rho L_di_q)^2<(\frac{|u_s|_{max}}{\omega_r})^2\\ 其中:\,\,凸极系数\rho=\frac{L_q}{L_d} \end{gather*} \]
得到电压极限椭圆:电压极限圆的两轴长度与电机转子角速度成反比,即随着速度的增大形成了逐渐变小的一簇套装椭圆(对于表贴式而言还是圆)
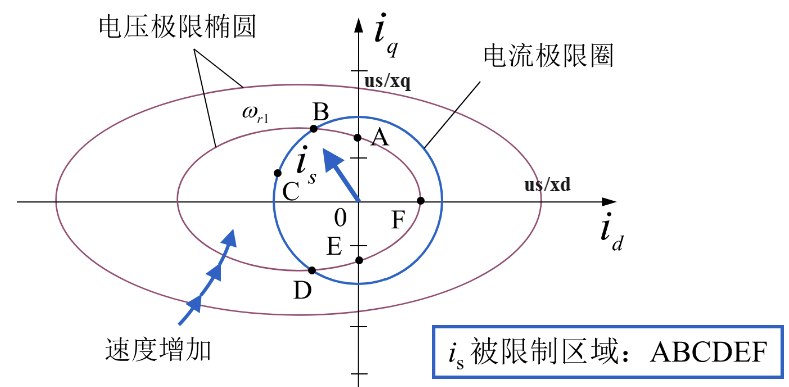
定义:
基速:空载电动势\(e_0\)达到电压极限值时的转子速度
- \[ \omega_{rb}=\frac{|u_s|_{max}}{L_mi_f} \]
转折速度:在恒转矩运行区,当定子电流为额定值,定子电压达到极限值时的转子速度
- \[ \omega_{rt}=\frac{|u_s|_{max}}{\sqrt{(L_mi_f)^2+(L_si_{sN})^2}} \]
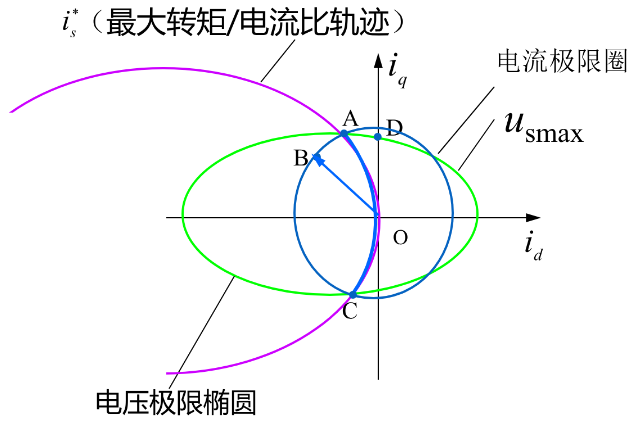
A-C段:电流调节器不饱和
电流矢量指令\(is\)处在电压椭圆之内,此时逆变器直流电压大于电机线电压,电流可控逆变器(通过电流调节器)迫使实际电流\(is\)跟随指令电流\(is^*\)。
A点:电流调节器饱和
电流矢量指令\(i_s^*\)处在电压椭圆之上,逆变器直流电压等于电机线电压,电流调节器饱和,逆变器失去电流控制能力
A-B段:调节器脱离饱和,弱磁控制
\(i_q\)逐渐减小,负向的\(i_d\)逐渐增大,此时\(i_d\)起去磁作用,转速逐渐上升
在极限时刻,\(i_q\)减小至0,最大转速可由电压极限椭圆方程计算得出:
\[ \omega_{r\,max}=\frac{|u_s|_{max}}{L_{md}i_f-L_d|i_d|} \]
通常\(|i_d|\)不可能太大,一是受电流极限圆的限制,二是防止对磁钢的去磁;其次,\(i_f>|i_d|\),\(L_{md}\)与\(L_d\)近似相等。因此,电机转速不会增至无穷大,一般为基速的2~3 倍左右。
弱磁控制方式
电流控制型:
| 查表法 | 梯度下降法 | 负直轴电流补偿 | |
|---|---|---|---|
| 实现方式 | 根据磁链、转矩和电流之间的关系来实现弱磁控制 | 通过电压极限椭圆的电压递减方向和恒转矩运行曲线方向之间的夹角大小来确定电机的弱磁区域 | 根据PI电流环输出的参考电压矢量幅值和给定电压幅值的差值,经PI调节器之后产生d轴弱磁电流,来达到弱磁效果 |
| 图片 | 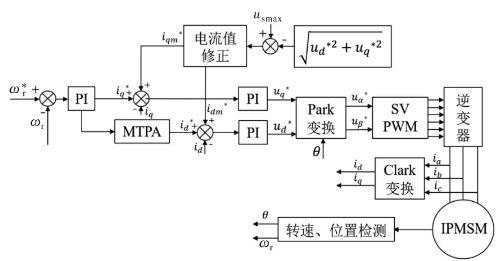 | 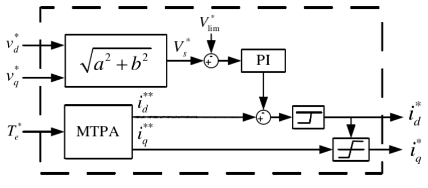 |
电压控制型:
| 固定交轴电压单电流调节器 | 变交轴电压单电流调节器 | |
|---|---|---|
| 实现 方式 | 交轴电压uq为定值,取代了交轴电流调节器的作用,根据电机的负载大小引入固定电压值 | 在定交轴电压法基础上进行优化,将定交轴电压的固定值变为随着实际转速与负载转矩变化的变化值 |
| 图片 | 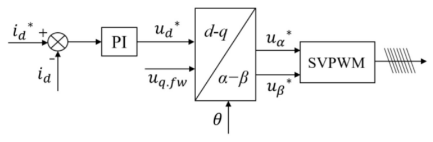 | 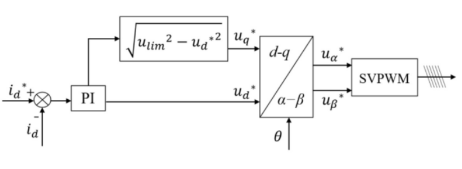 |
相角控制型:超前角弱磁控制
- 通过控制超前角β的大小来实现弱磁控制
- 当电机转速小于基速时,参考电压幅值低于给定电压幅值时,弱磁环节未发生作用,超前角为0,系统运行在恒转矩模式,此时相当于id=0控制;
- 当超过给定电压幅值时,弱磁环节开始作用,超前角值为负,此时d轴参考电流为负,进行弱磁控制
弱磁控制框图
负直轴电流补偿
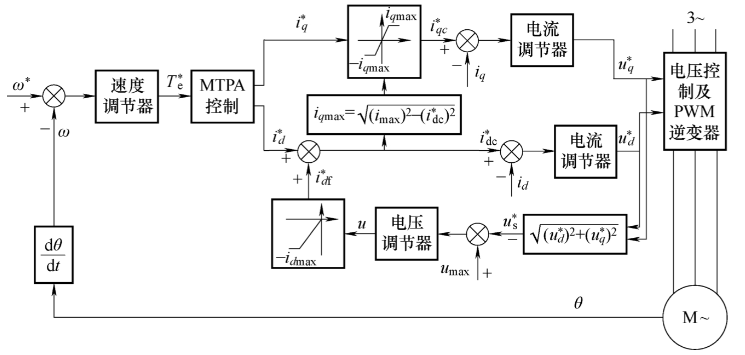
- 本质:通过电压环VT(PI)计算补偿电流\(i_0\)
详细解释一下,正常的MTPA是通过\(T_e^*\)输出\(i_d^*\)和\(i_q^*\)。而PMSM的弱磁控制需要给他增加额外的负直轴电流,那新增的这部分电流肯定是通过电压环VT(PI)来实现的,所以有这么一个“最大电压 - 观测电压 → PI环节”得到负直轴电流的环节。然后把这部分电流拿去减原本的\(i_d^*\)得到真正的\(i_d^*\),并通过限幅得到真正的\(i_q^*\)。
直接转矩控制
- 矢量控制从理论上解决了交流调速系统的静、动态性能问题 ,其动态性能好,调速范围宽。
- 但实际应用中,转子磁链难以准确观测,系统特性受电动机参数影响较大,另外在模拟直流电动机控制过程中所用矢量旋转变换的复杂性(当时算力还不够)使得实际控制效果难以达到理论分析的结果。
- 转矩和磁链的控制采用Bang—Bang控制器,并在PWM逆变器中直接用这两个控制信号产生电压的PWM波形,从而避开了将定子电流分解成转矩和磁链分量,省去了矢量旋转变换和电流控制。
- 选择定子磁链作为被控量,而不像FOC系统那样选择转子磁链,计算磁链的电压模型不受转子参数变化的影响。
异步电机DTC
- 说明:根据个人的理解,定子电压六边形向量的具体位置是跟电压源逆变器的结构、电压矢量的规定方向有关的:
- 在年珩的《电机控制》中:电压源逆变器的开关值分别为E和0,电压矢量a相与\(\alpha\)轴重合,画的是相电压。
- 在孙丹的课件PPT中:电压源逆变器的开关值分别为E/2和-E/2,电压矢量\(V_{ab}\)与\(\alpha\)轴重合,画的是线电压。
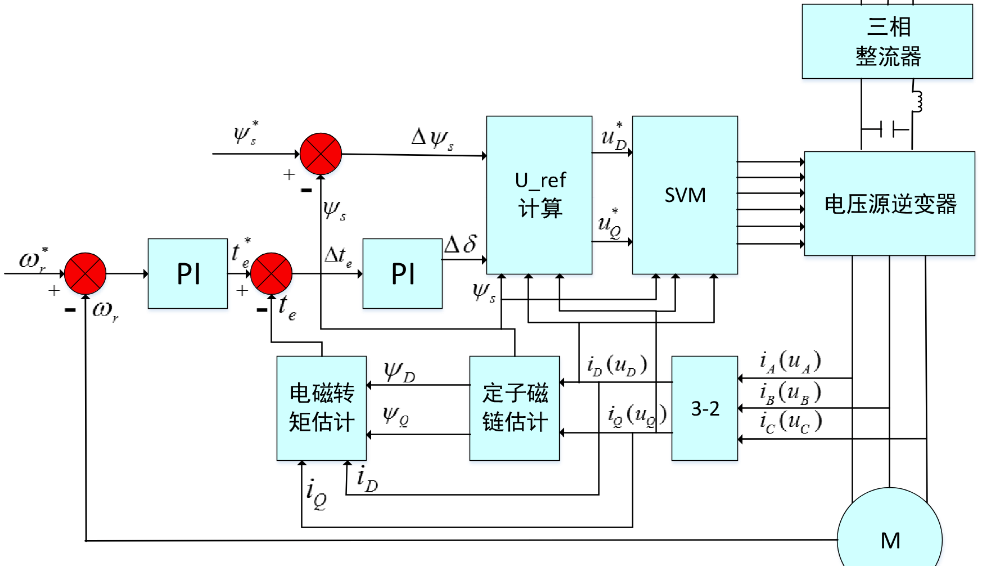
- 本教程以年珩《电机控制》中的六边形电压向量图为准:
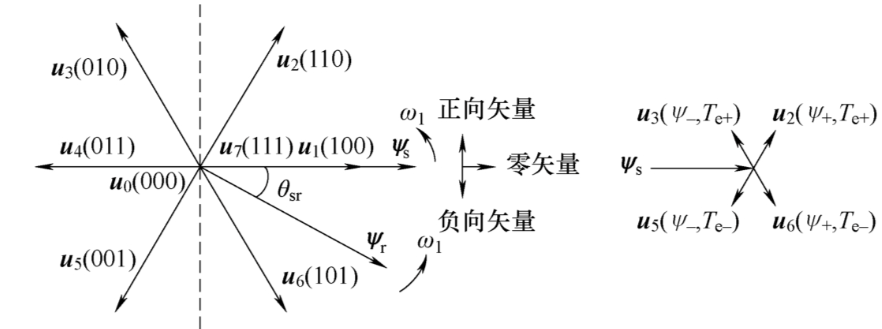
在忽略定子压降的情况下,定子磁链和电压的关系可以表示为:定子磁链的变化就是定子电压×作用时间
\[ \psi_s=\int(u_s-R_si_s)\text dt\Rightarrow\Delta \psi_s=u_s\Delta t \]
电磁转矩的公式:(书里没有二分之三,应该是他写错了,但是不重要)
\[ T_e=\frac 32p(\psi_{s\alpha}i_{s\beta}-\psi_{s\beta}i_{s\alpha})=\frac{K_T}{L_m}\psi_s\psi_r\sin\theta \]
其中:\(\psi_s\)走走停停, \(\psi_r\)均速运行,夹角不断变化,电磁转矩脉动。但是一般可以认为:在一个开关周期内,转子磁链\(\psi_r\)变化很小,近似不变,所以直接调节定子磁链\(\psi_s\)。
定子磁链观测
与交流电机矢量控制中的转子磁链定向类似,DTC的定子磁链也有相应的观测器
| 电压模型观测器 | 电流模型观测器 | |
|---|---|---|
| 输入 | 定子电压 \(u_{s\alpha\beta}\)、定子电流 \(i_{s\alpha\beta}\) | 定子电流 \(i_{s\alpha\beta}\)、电机转速 \(\omega_r\) |
| 过程 | \(\begin{gather*}\psi_{s\alpha}=\frac1p(u_{s\alpha}-R_si_{s\alpha}) \\\psi_{s\beta}=\frac1p(u_{s\beta}-R_si_{s\beta}) \end{gather*}\) | 跟转子磁链定向一样 \(\begin{gather*}\psi_{r\alpha}=\frac{1}{T_rp+1}[L_mi_{s\alpha}-\omega T_r\psi_{r\beta}]\\\psi_{r\beta}=\frac{1}{T_rp+1}[L_mi_{s\beta}+\omega T_r\psi_{r\alpha}] \end{gather*}\) |
| 输出 | \(\begin{gather*}\psi_{s\alpha}\\ \psi_{s\beta}\end{gather*}\) | \(\begin{gather*}\psi_{s\alpha}= \sigma L_si_{s\alpha}+\frac{L_m}{L_r}\psi_{r\alpha}\\ \psi_{s\beta}= \sigma L_si_{s\beta}+\frac{L_m}{L_r}\psi_{r\beta} \end{gather*}\) |
| 优点 | 中高速准确 | 中低速准确 |
| 缺点 | 对电机参数变化敏感 | 对电机参数变化敏感 |
控制框图
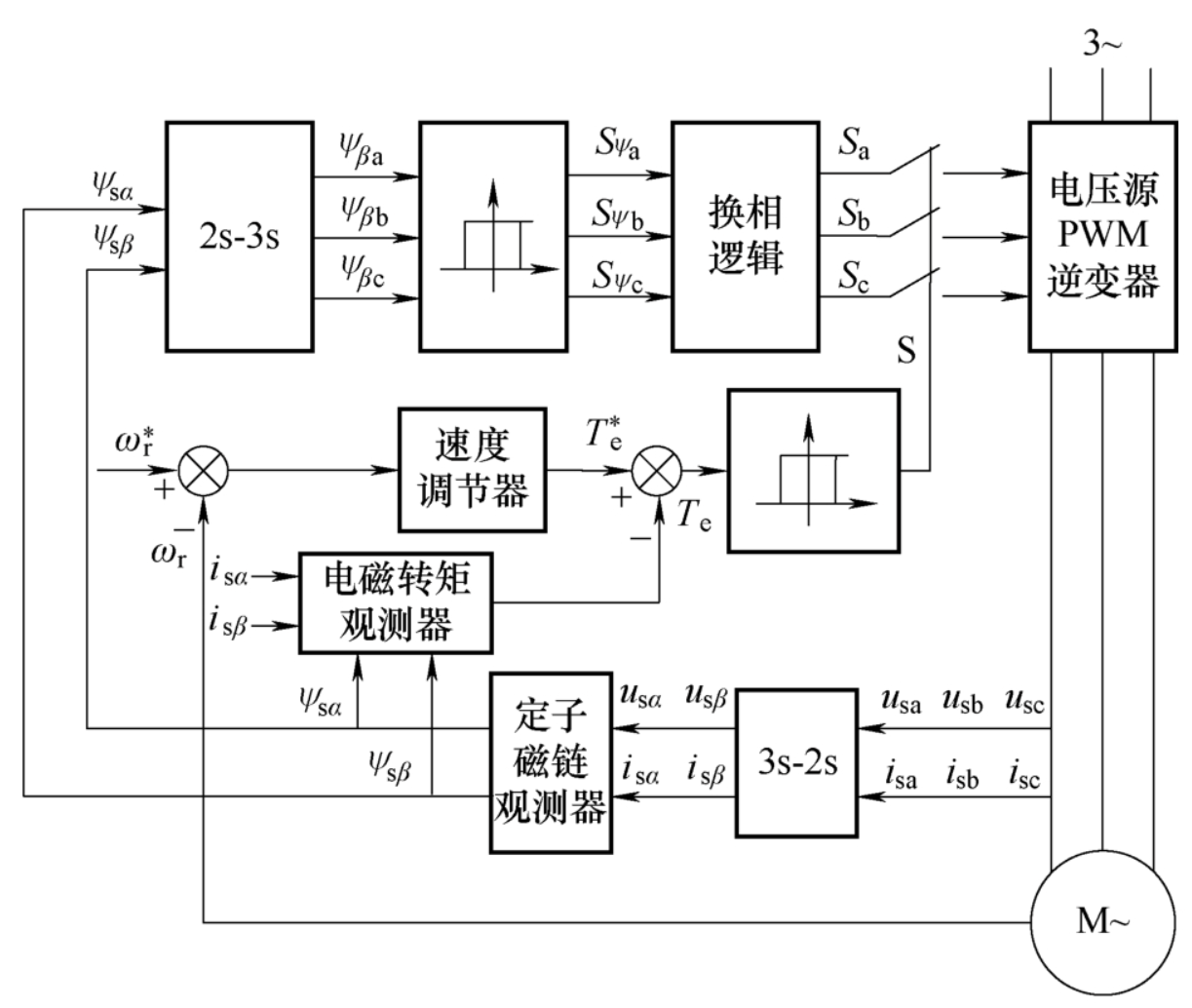
其中换向逻辑的推导方式如下:
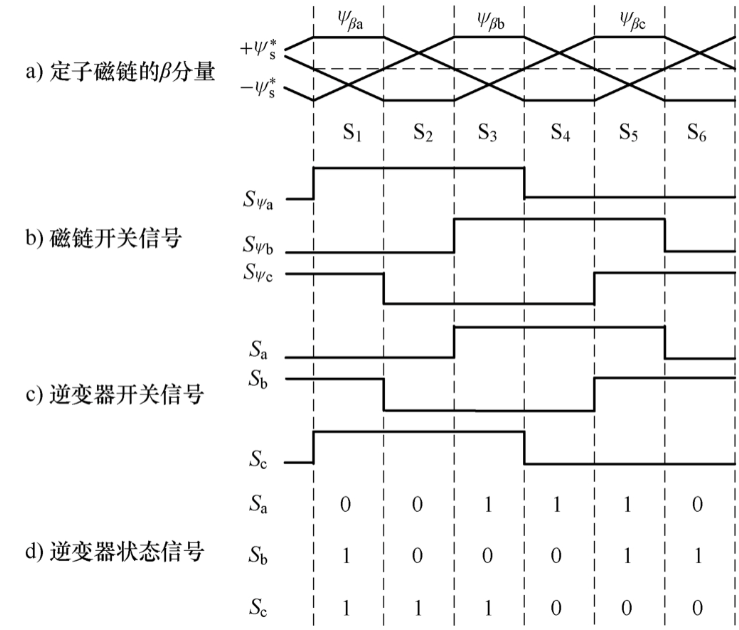
正转换向逻辑:
- \[ \begin{gather*} S_{\psi a}=S_c\\S_{\psi b}=S_a\\S_{\psi c}=S_b \end{gather*} \]
反转换向逻辑
- \[ \begin{gather*} S_{\psi a}=S_a\\S_{\psi b}=S_b\\S_{\psi c}=S_c \end{gather*} \]
其中:\(S_a\)表示逆变器a相的开关状态,\(S_{\psi a}\)表示a相磁链经过滞环控制器后的状态
恒转矩与恒功率控制
与交流电机的普通变频控制一致,DTC也遵循基频以下恒转矩(磁通保持不变),基频以上恒功率(磁通随频率减小)的基本原则。
基频以下
此时定子磁链保持恒定值不变,频率\(f<f_N\),磁链幅值的计算方式为:
- \[ \psi_s=U_NT_s=\frac{U_N}{2\pi f_N} \]
当转速刚好等于同步速(基频)时,磁链形成六边形,每个电压空间矢量正好轮流作用六分之一个周期
但是,当转速小于同步速时,如果仍然这么做,那么定子磁链速度(基频)将会快过转速(转子磁链速度),两磁链运行速度不同,根据电磁转矩的公式,只能有脉动转矩
因此,必须在6个电压空间矢量运行的过程中,加入零电压矢量,主动调节定子磁链的运行速度。
基频以上
- 基频以上之后,如果保持定子磁链幅值不变,那么由于电压无法增大,它走一圈的周期仍然是同步速周期。此时转速(转子磁链速度)将会快过定子磁链速度(基频),同样无法形成有效电磁转矩。
- 所以,为了让定子磁链转动的更快,必须让他幅值变小(定子磁链轨迹是个圆,电压空间矢量在圆周上一直以基频运动,圆半径变小,运行周期就变短了)
- 变化方式:恒功率,所以直接和速度成反比
自动切换
我看不懂
圆形磁链轨迹控制
六边形磁链轨迹控制时,磁链的切换是通过换向逻辑进行开环控制,而现在则需要通过滞环的磁链环FT进行闭环控制。
将磁链给定值和磁链观测值作差:
\[ \Delta \psi_s>\varepsilon_{\psi_s}\Rightarrow S_{\psi}=1\Rightarrow 需要减小磁链幅值 \]
\[ \Delta \psi_s<\varepsilon_{\psi_s}\Rightarrow S_{\psi}=0\Rightarrow 需要增大磁链幅值 \]
由此得到\(4\times6\)的逆变器开关状态表:
- 4列:由磁链滞环控制信号\(S_{\psi}\)(2状态)和转矩滞环控制信号\(S_T\)(2状态)组合
- 6行:定子磁链的扇区,每个扇区匹配的定子电压空间矢量自然是不同的
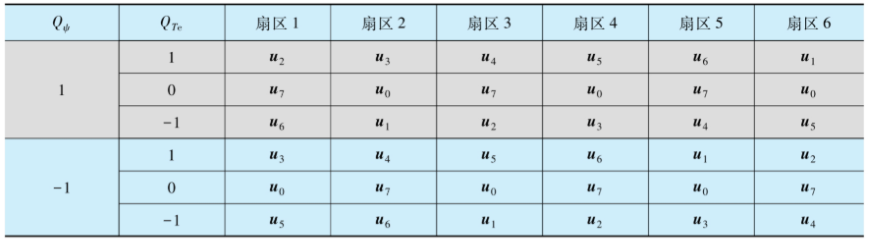
- 当然这里变成\(6\times6\)的了,是他把转矩滞环控制信号\(S_T\)拓展成了3状态,本质差不多。
永磁同步电机DTC
类似的,有:
\[ T_e=\frac32\frac1{L_s}p\,\psi_s\psi_f\sin\theta \]
若保持定子磁链幅值\(|\psi_s|\)恒定,则永磁同步电机电磁转矩与\(\sin\theta\)成正比。即可通过控制定子磁链幅值恒定,改变定子磁链旋转速度和方向来瞬时调整转矩角,实现转矩的动态控制,这正是直接转矩控制的基本思想
不是我™搞不明白同样的东西她PPT里放两遍干嘛
空间矢量调制DTC
原本:逆变器只提供八个基本电压空间矢量,且在一个甚至多个采样周期中逆变器开关状态始终保持不变。
现在:引入了空间矢量调制方法(SVM),根据实际需要的电压矢量,对逆变器提供的八个基本矢量进行调制,即采用两种以上有效空间矢量及零矢量,按需要的时间长短作用,以最终获得所期望的空间矢量
基本原理:把任意一个电压矢量分解为矢量所在扇区相邻的两个开关电压矢量和零矢量
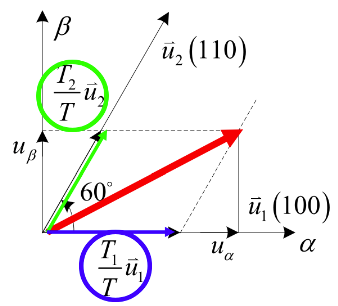
\[ \vec {u_s}=\frac{T_1}T\vec {u_1}+\frac{T_2}T\vec{u_2} \]
由于这个时候需要准确的磁链位置来使系统能够计算所需的电压,因此使用普通的转矩环(PI)和磁链环来代替滞环。(所以这个时候没有滞环了)
开绕组与双三相电机
这部分考试基本不考,仅做了解(因为我们这届被国庆冲了一节课,没冲的话不好说)
开绕组PMSM
大概拓扑就是:三相变压变流器 - 电机 - 三相变压变流器(把原本电机中连在一起的三相绕组中性点打开,Y连接的连接处换成了三相变压变流器),能达到更大的功率,并放开零序电流。
- 多种控制方法
- 电压二分法
- 交替钳位法
- 统一空间矢量调制法
- 共直流母线型
常规的控制方式就是在原有FOC/DTC的基础上,将\(u_{\alpha}/u_{\beta}\)经过开关控制输入到逆变器这一环节复制一份,形成两份开关表,分别送到电机两端的两个三相变压变流器(逆变器)中。
双三相PMSM
低压大功率输出
永磁同步电机模型预测控制MPC
- 优势:控制思想直观、处理多约束能力强、动态响应快、多目标优化灵活
- 思路:预测模型、滚动优化、反馈校正
- 分类:与永磁同步电机的FOC策略与DTC策略结合
- MPCC:使用模型预测控制器代替FOC中的电流环PI控制器
- MPTC:使用模型预测控制器的定量控制代替DTC中滞环控制器的定性控制
- MPFC:使用模型预测控制器的定量控制代替DTC中定子磁链滞环控制器的定性控制
- 本质:对系统未来状态变量的预测;在系统当前状态的基础上,根据代价函数最小化原则,在控制集范围内对控制结果进行评估,从而得到最优控制量(施加的电压矢量)并输出
- 控制:将传统控制器输出得到的Reference值(\(\,^*\))和模型预测得到的k+1时刻值共同输入到objFcn优化评估中。
代价函数 Cost Fcn
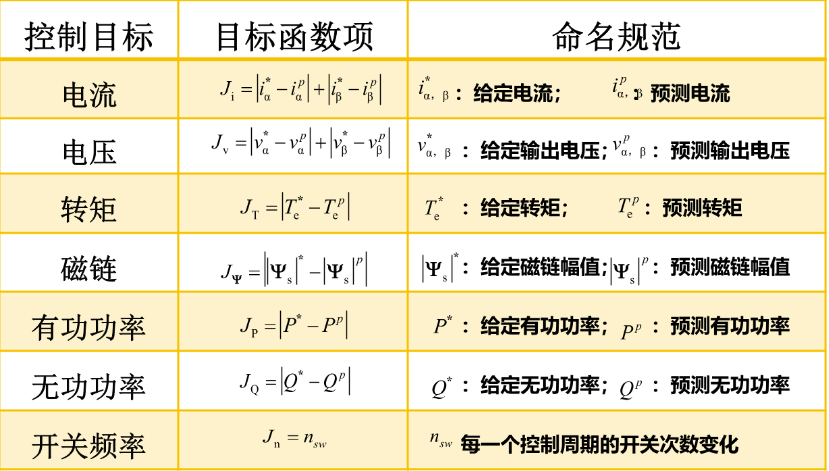
一般采用常规的权重法来平衡这一多目标优化问题:
\[ J=\sum_k\lambda_kJ_k \]
常见的代价函数采用预测值和给定值的一阶范数:
不同MPC控制策略
PMSM-MPCC
在转子磁场定向下建立的d-q坐标系,其中\(\psi_{rd}=\psi_r,\psi_{rq}=0\),对电机的电流状态方程式进行欧拉离散,得到预测方程
\[ i_{sq}(k+1)=f(i_{sd}(k),i_{sq}(k),u_{sq}(k))\,\,\,(i_{sd}类似) \]
得到以电流为控制目标的目标函数:
\[ J=|i_d^*(k+1)-i_d(k+1)|+|i_q^*(k+1)-i_q(k+1)| \]
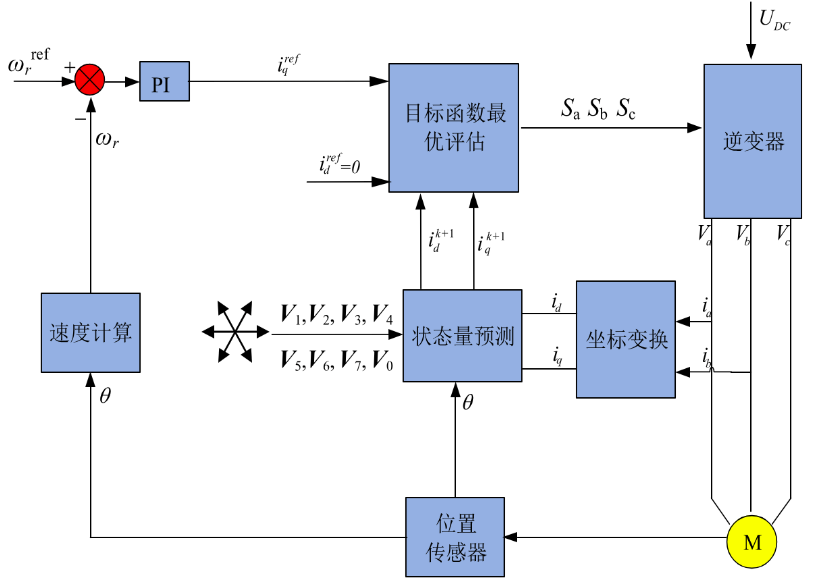
说明:
- 这里应该是表贴式PMSM,所以采用了\(i_d=0\)的FOC,如果要用MTPA的话也差不多
- 一次模型预测控制要计算7次,即分别带入7个电压开关矢量去(6个有效电压矢量+1个零矢量)计算代价函数\(J\)的大小并比较。
PMSM-MPTC
根据电机基本方程,选取状态变量\(i_{s\alpha},i_{s\beta},\psi_{s\alpha},\psi_{s\beta}\) ,并假定\(\omega(k)=\omega(k+1)\),可以得到电机定子磁链、电流和电磁转矩的欧拉离散公式:
\[ \begin{gather*} \psi_{s\alpha}(k+1)=f(\psi_{s\alpha}(k),i_{s\alpha}(k),u_{s\alpha}(k))\,\,\,(\beta一样)\\ i_{s\alpha}(k+1)=f(\psi_{s\alpha}(k),i_{s\alpha}(k),i_{s\beta}(k),u_{s\alpha}(k),u_{s\beta}(k))\,\,\,(\beta一样) \end{gather*} \]
得到以磁链和转矩为控制目标的目标函数:
\[ J_1=|T_e^*-T_e^{k+1}|+K_{\psi}|\psi_s^*-\psi_s^{k+1}| \]
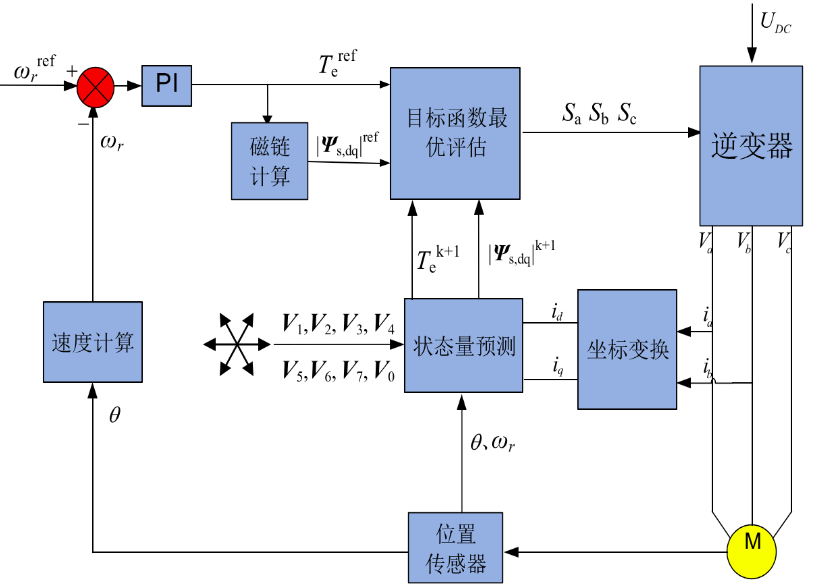
同样,一次模型预测控制要计算7次,即分别带入7个电压开关矢量去(6个有效电压矢量+1个零矢量)计算代价函数\(J\)的大小并比较。需要调节因子系数整定工作;对系统参数依赖大。
PMSM-MPFC
改进评估函数,消除调节因子系数,提出模型预测磁链控制
\[ \varPsi_{s,dq}^*=\psi_f+j(L_qT_e^*/1.5N_p\psi_f) \triangleq \psi_d+j\psi_q \\ J=|\varPsi_{s,dq}^*-\varPsi_{s,dq}^{k+1} | \]
传统MPTC中转矩、定子磁链幅控制目标可以转化为对定子磁链矢量的单一控制
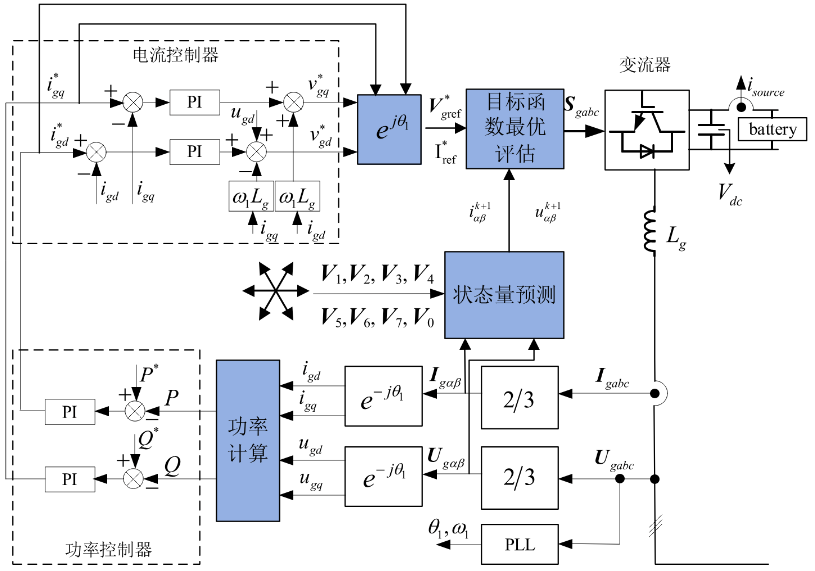
并网逆变器(网侧PWM)控制
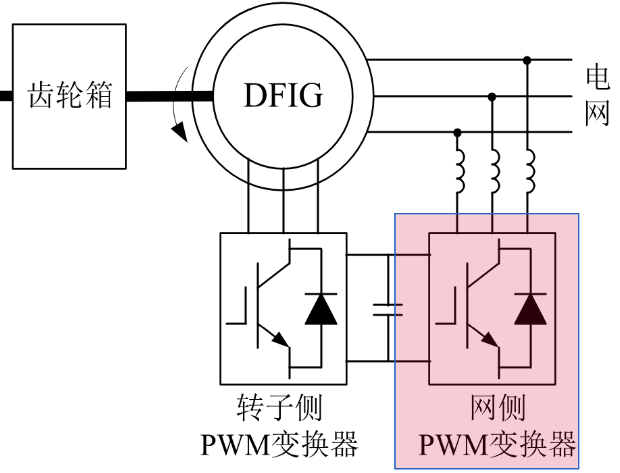 | 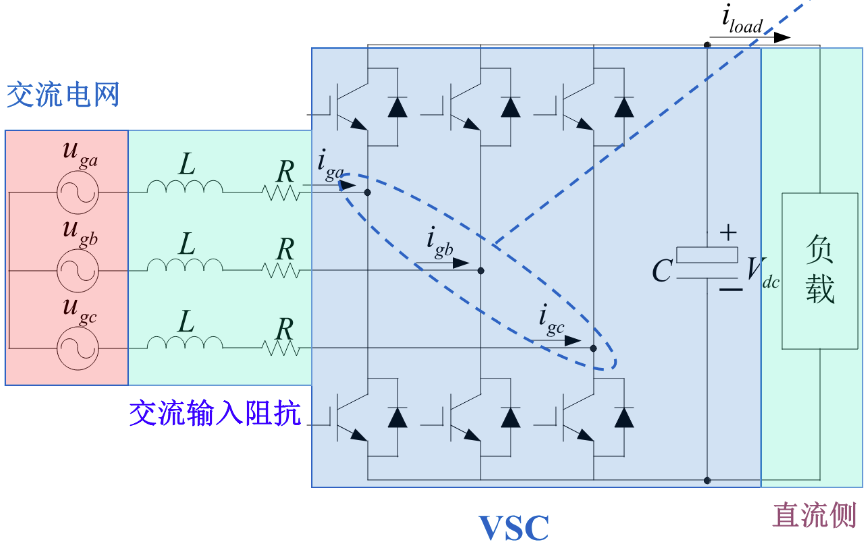 |
|---|
假设三相电网电压对称,将坐标系d轴定向于电网电压矢量,稳态时各状态变量的导数等于零,得到:
\[ \begin{gather*} u_{gd}=& \sqrt{\frac32}U_g&=Ri_{gd}-\omega_1Li_{gq}+v_{gd}\\ u_{gq}=& 0&=Ri_{gq}+\omega_1Li_{gd}+v_{gq} \end{gather*} \]
负载电流:
\[ i_{load}=(S_di_{gd}+S_qi_{gq})-C\frac{\text dV_{dc}}{\text dt} \]
- 并网逆变器的主要的功能是保持直流母线电压\(V_{dc}\)的稳定、输入电流正弦和控制输入功率因数。
- 并网逆变器的控制本质是控制瞬间流入流出的有功和无功功率
- 对交流侧有功功率 \(P\) 的控制实际上就是对输入电流有功分量 \(i_{gd}\) 的控制
- 对交流侧无功功率 \(Q\) 的控制实际上就是对输入电流有功分量 \(i_{gq}\) 的控制
- 整个网侧PWM变换器的控制系统可以分为两个环节:电压外环控制及电流内环控制
\[ \begin{gather*} \begin{bmatrix} P\\Q \end{bmatrix}=u_{gd}\begin{bmatrix} i_{gd}\\-i_{gq} \end{bmatrix} \end{gather*} \]
矢量控制VOC
- 将VSC网侧交流电流分解成有功、无功分量,采用2个PI电流调节器控制2分量电流,实现有功、无功功率的间接控制
- 在网侧PWM变换器的电流控制中,以电网电压矢量d轴定向的电压电流双闭环控制最为广泛
- 缺点:
- 有复杂的坐标旋转变换
- 电流调节器整定难,特性受运行状态变化大
- 电网电压不平衡时必须分解成正负序两套系统下实施d-q解耦控制
- PI为线性控制器难满足非线性系统的优化控制
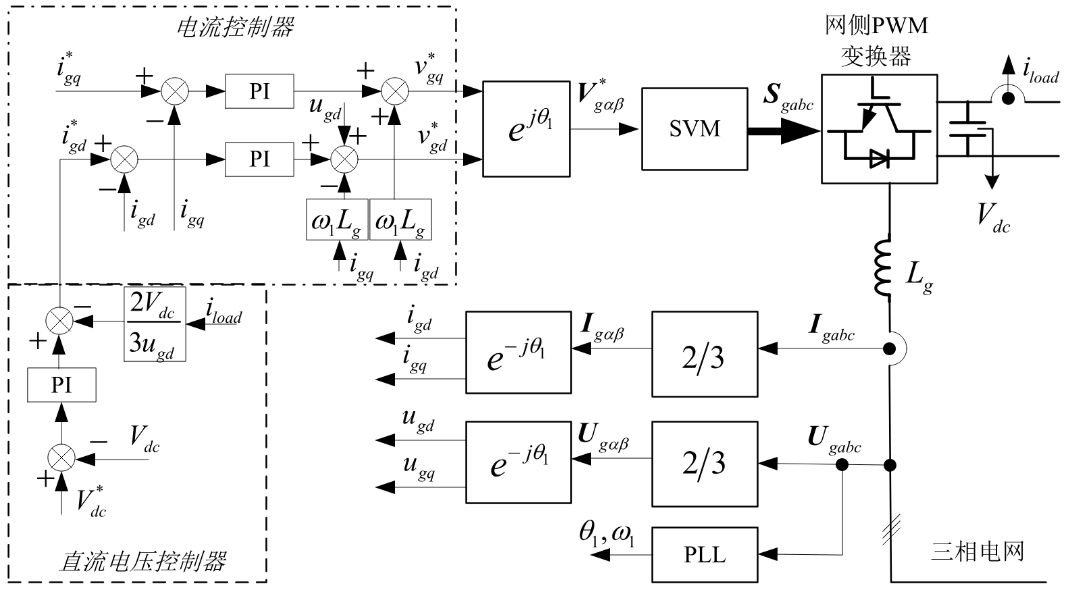
直接功率控制DPC
- 根据:
- 瞬时有功、无功功率的误差
- VSC交流侧电压矢量的空间位置
- 采取二位滯环调节器,从优化的开关表中选择VSC三相开关状态(即电压空间矢量),直接控制产生的瞬时功率大小,达到消除功率误差的目的
- 优点:
- 功率调节动态响应快
- 无需矢量旋转变换、线性PI调节器及其引发缺陷
- 能适应不平衡电压下的控制
- 缺点:
- 静态性能优劣取决滯环调节器带宽,有静动态特性矛盾
- VSC开关频率不恒定,带来滤波器设计困难、电流波形畸变、损耗发热及冷却有问题
- 动态性能还与电网、负载及运行工况有关
\[ \begin{gather*} \text p\begin{bmatrix}P_s\\Q_s \end{bmatrix}=\frac32\frac1{L_s}\omega_1\psi_{sd}\,\,\text p\begin{bmatrix}-\psi_{cq}\\\psi_{cd} \end{bmatrix}=\frac32\frac1{L_s}\omega_1\psi_{sd}\,\,\begin{bmatrix}-V_{cq}\\V_{cd} \end{bmatrix} \end{gather*} \]
- 控制所施加的电压矢量, 可控制VSC磁链\(\psi_c\)的变化;
- 磁链矢量沿所施加的电压矢量方向运动, 运动速度正比于电压矢量的大小
- 查表
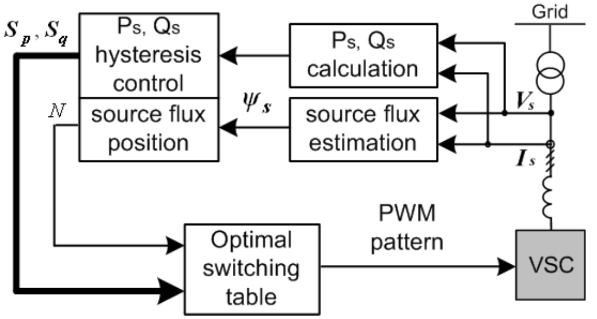
模型预测控制MPVOC
- 优点:
- 直接计算最优开关状态,没有内环PI调节器和调制器的延迟,因此动态响应极快
- 多目标控制、处理约束方便
- 缺点:
- 计算负担重、没有固定的开关频率
- 依赖模型精度,对电机参数变化敏感
根据在k时刻的瞬时电压、电流,可得k+1时刻的瞬时电压、电流。目标函数可以电压、电流的指令值与反馈值的误差平方为基础:
\[ G=\lambda_1[i_L(k+1)-i_{L,ref}]^2+\lambda_2[u_c(k+1)-u_{c,ref}]^2 \]
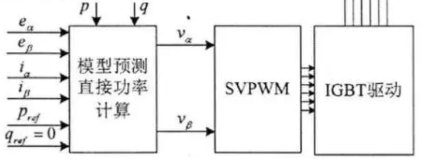
模型预测控制MPDPC
直接功率控制DPC当然是要直接控制系统功率,所以代价函数为有功指令值与反馈值误差的平方、无功指令值与反馈值误差的平方之和。其中系统有功指令是直流母线PI控制器的输出与母线电压的乘积,无功功率为0。
\[ G=\lambda_1[p_{ref}-p(k+1)]^2+\lambda_2[0-q(k+1)]^2 \]
通过对代价函数推算求得最优电压矢量,将最优电压矢量送入SVPWM 模块,实现了功率内环的最优控制
参数辨识与无传感器控制
主要讲离线辨识
定子电感——高频信号注入法
将转子堵转,并向定子注入高频旋转电压信号,根据高频电流响应提取定子电感
向定子通入高频电压矢量\(U_{sh}\),频率较高时,忽略电阻压降,将转子堵转,使反电势为0。通过提取电流的正负序分量可以分别计算得到直轴和交轴电感
定子磁链——反电势提取法
根据空载恒转速条件下反电势与转子磁链的线性关系计算转子磁链
空载时,可近似认为端电压等于反电势。采用矢量控制方案使电机以恒定转速空载运行,测量此时的给定电压指令,计算出转子磁链:
\[ \psi_f=u_s/\omega_e \]
转动惯量
人工轨迹法
在恒负载条件下,忽略摩擦系数,给定两个不同的转矩电流,可以得到两个机械运动方程。
设置控制器参数使电机进行匀加速或匀减速运动,计算不同转矩下的加速度,通过离散化作差可以计算出转动惯量。
自由减速法、限转矩幅加速度法
转动惯量的离线辨识都是特定的条件下测量转速的响应,再根据机械运动方程实现辨识,三种方法原理类似
高频信号注入法 - 旋转高频电压
在电机出线端注入一个三相平衡的高频电压(或电流)信号,利用电机内部固有的或人为的(如对电机进行改造)不对称性,使电机产生一个可检测的磁凸极,通过检测对应的高频电流(或电压)响应来获取转子位置和速度信息。
- 高频信号注入法的特点:
- 在观测器的带宽内,观测器对转动惯量的误差不敏感,因此跟踪观测器必须有足够的带宽
- 凸极模型为一个相位和估计的转子位置角(电角度)有关的单位矢量,凸极跟踪过程与负相序高频电流分量的幅值大小没有直接的关系,因此对电机参数的变化不敏感
- 观测器的机械系统模型中电磁转矩的前馈输入使得观测器在跟踪过程中没有滞后,即具有零滞后特性
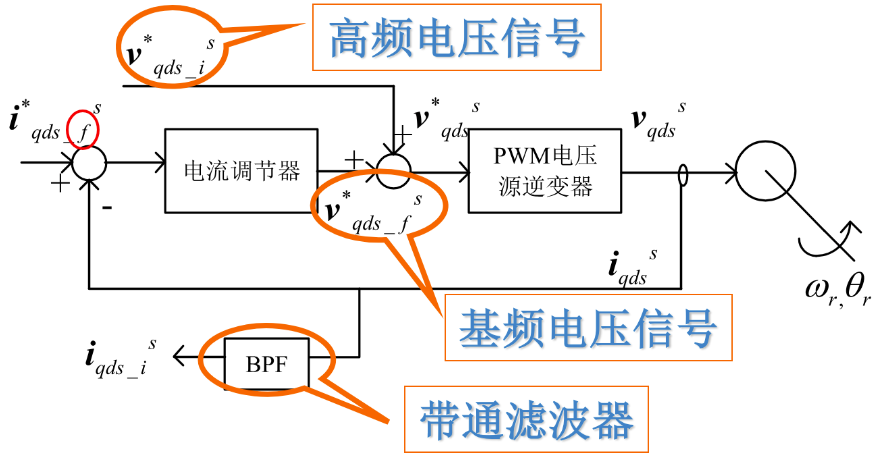
经过一通化简,反正得到:只有负相序高频电流分量的相位中包含转子位置信息
\[ i_{qdi}=i_{ip}e^{(\theta_i(t)-\pi/2)}+i_{in}e^{(2\theta_r-\theta_i(t)+\pi/2)} \]
把高频电流矢量通过坐标变换,变换到一个与注入的高频电压矢量同步旋转的参考坐标系中,正相序高频电流矢量变成直流,通过常规的高通滤波器予以滤除。下图是嵌入式PMSM的旋转高频电压注入法矢量控制框图
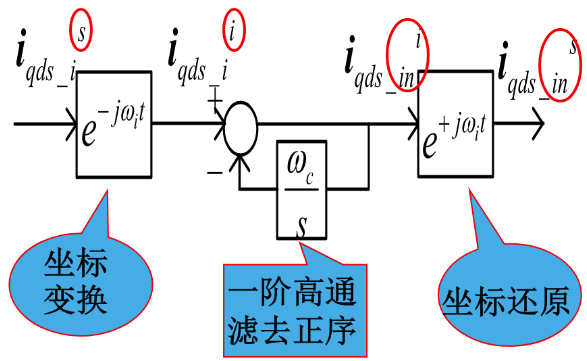
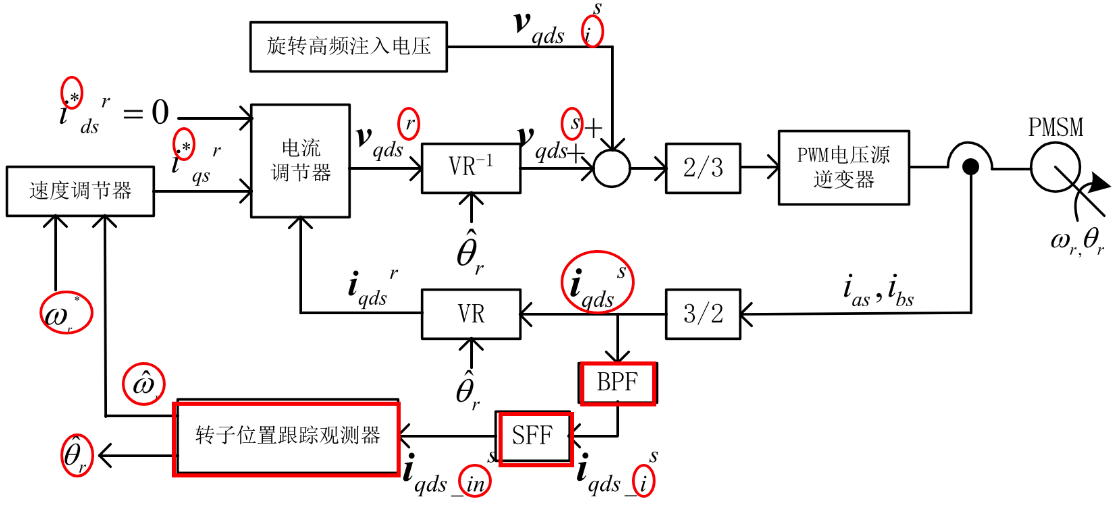
过程解释如下:
- 在定子电压中注入高频旋转电压信号(dq)
- 从定子电流检测值中进行读取
- 经过带通滤波器BPF得到高频旋转电流信号\(i_{qds\_i}^i\)
- 经过同步轴系高通滤波器SPF得到电流的负序分量\(i_{qds\_in}^i\)
- 从(转子位置跟踪观测器)中读取转子转速和位置
转子位置自检测 - 参考模型自适应法(MARS)
只根据注入的高频电压和凸极相互作用产生的高频电流信号无法正确区分电机的N极和S极
MARS法的基本思想:
- 具有相同物理意义输出量的模型:同时工作,利用输出量的差值,根据合适的自适应率来实时调节可调模型的参数,以达到控制对象输出跟踪参考模型的目的
- 可调模型:含有待估计参数的方程
- 参考模型:不含未知参数的方程
- 自适应率:比如PI,将差值经自适应率后返回可调模型
- 优势:
- 模型参考自适应法是基于稳定性设计的参数辨识方法,能保证参数估计的渐进收敛,具有良好的动态性能。适合中高速运行。
- 劣势:
- 对电机参数的变化比较敏感。低速时会由于电流检测和参数估计精度的限制, 及逆变器非线性的影响,导致转子速度和位置无法精确估计
定子电流数学模型
- 参考模型:PMSM电机本体(反馈检测到电流?)
- 可调模型:电流模型(采用电阻电感计算到的电流?)
- 采用并联型结构辨识转速
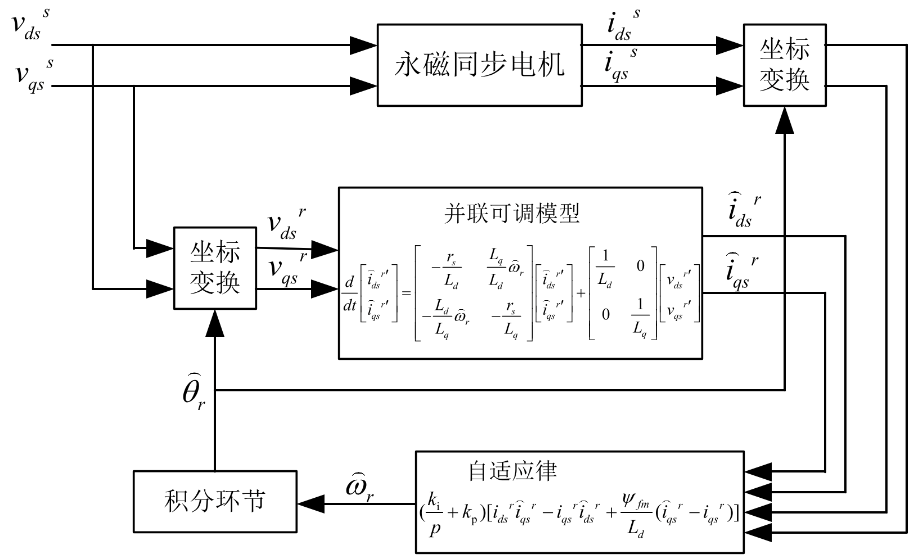 | 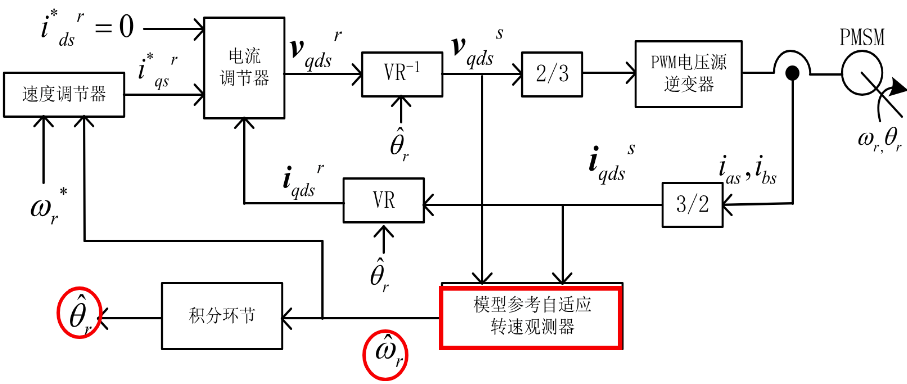 |
|---|---|
| 局部模型 | 整体模型 |
- 当然,可以采用中低速时使用高频信号注入、中高速时使用MARS法,中速段用线性变化的权重共同作用的方式控制。