电机控制
PDF看这个:电机控制笔记PDF版本
直流电机的控制
晶闸管与双闭环调速
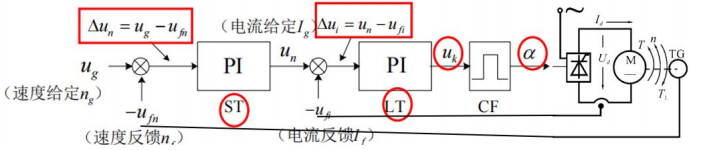
PI调节器的作用:
- 速度调节器 ST:
- 调速精度,做到静态无差;使机械特性硬,满足负载要求;
- 实现转速快速调节。
- 电流调节器 LT:
- 精确满足负载转矩大小要求;
- 调速的快速动态特性(转矩的快速响应)。
- 速度调节器 ST:
电流环在内的原因:
- 时间常数小,响应更快
- 引入电流环是为了控制电枢电流
- 电流仅与负载转矩有关
PI参数的影响:
Kp增大,提高系统动态性能;反之削弱
Ki增大,静态误差减少,但系统容易震荡;
Ki减小,积分太弱,稳态误差难以快速减小
Kd过大或过小,增加系统超调和调节时间
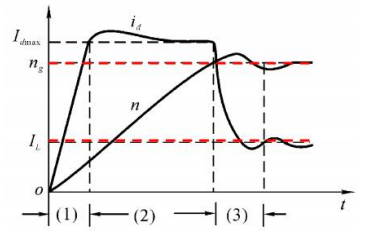
起动过程特征:
起动:\(i_d\) 由 0 上升到 \(I_{d \,max}\)(限幅值);
ST、LT 全部饱和限幅,蜕化为限幅器,系统实为速度、电流双开环;
加速:\(i_d=I_{d \,max}\) 恒定(电流调节结果,非限幅);
ST 饱和限幅,LT 作 PI 调节,实为电流单闭环系统
PI 调节至稳态: 转速稳定至 \(n=n_g\),电流稳定至 \(i_d=I_L\)(对应 \(T_L\));
ST、LT 均作 PI 调节,真正速度、电流双闭环工作。
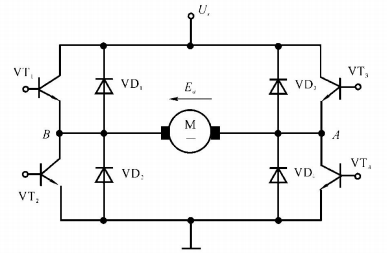
PWM调速
 |  |
|---|
| 单极性 | 双极性 | |
|---|---|---|
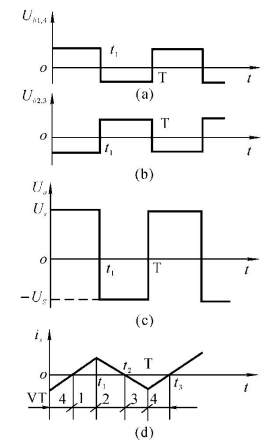
| 工作 方式 | 1. VT3关断,VT4导通 2. VT1 和 VT2 轮流导通 3. 控制电压为负时,13对调,24对调 | 1. VT1 和 VT4 同极性 2. VT2 和 VT3 同极性 3. 两组极性(通断)互补 |
| 负载电压系数 | \(\rho=D\) | \(\rho=2D-1\) |
| 工作 流程 | 1. VT1 通,电动运行 2. VD2 蓄流,电动运行 3. VT2 和 VD4 导通,能耗制动 4. VD1 和 VD4 蓄流,再生制动 | 1. VT1 和 VT4 导通,电动运行 2. VD2 和 VD3 蓄流,电动运行 3. VT3 和 VT2 导通,反接制动 4. VD4 和 VD1 蓄流,再生制动 |
异步电机的控制
调速主经常使用“转差功率不变型”调速方式,即保证 s (\(P_s\))不变。如异步电机的变频调速和变极调速均属于这类方式。
还有“转差功率消耗型”调速方式,通过消耗转差功率 \(P_{s}=sP_e\) 来换取转速的下降,如调压调速,串电阻调速。
变转差调速
调压调速
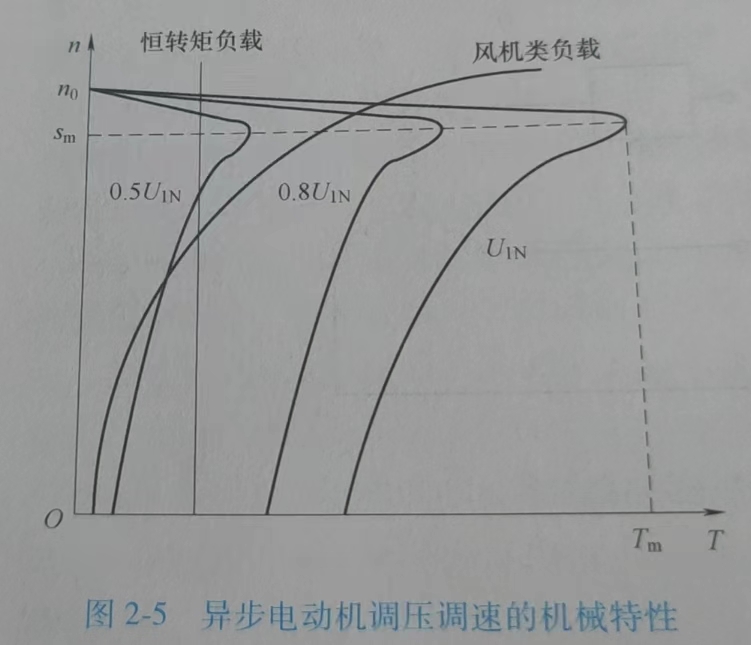
- 电机电磁转矩:\(T_e\propto U^2\)
- 缺点:调速范围较小(\(s\in(0,s_m)\))。只能降压调速,且\(\phi_m=\frac{U_1}{4.44K_{dp}f_1N}\),属于弱磁调速。依靠增大转差频率 s 调速,转子回路消耗的滑差功率增大,机械输出功率减小。
串级调速
串级调速是指在转子中引入与转子同频(\(sf_1\))的转子电势,以吸收或补充滑差功率,从而进行调速。详见第三章。
变频调速
变频调速的理论基础
基本实现方法
\[ T_m\propto\frac{U_1^2}{\omega_1} \]
| 基频下调 | 基频上调 | |
|---|---|---|
| 要求 | 保持气隙磁通 \(\phi_m\) 恒定→磁路工作点不变 变频中维持 \(E_1/f_1\) 为定值 适合恒转矩负载 | 定子电压 \(U_1=U_{1N}\) 属于弱磁调速,适合恒功率负载 |
| 机械特性 | 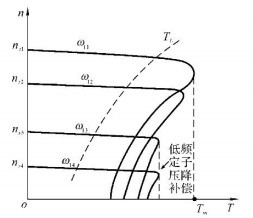 | 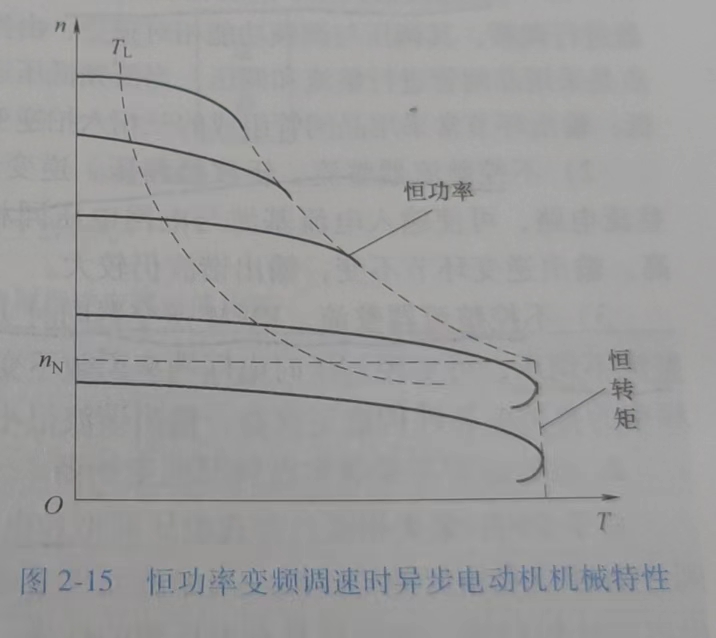 |
| \(\Delta n\) 不变,s-T向下平移 考虑阻感压降,\(T_m\propto f\) 下降 | \(\Delta n\) 变大,机械特性变软 气隙磁通↓ → 电磁转矩↓ |
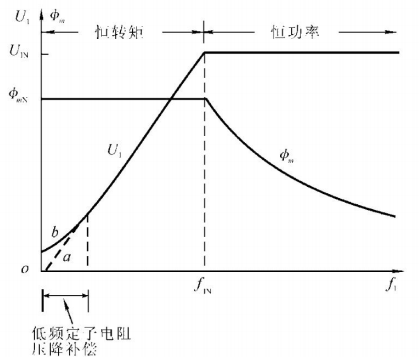
基频以下电压补偿控制
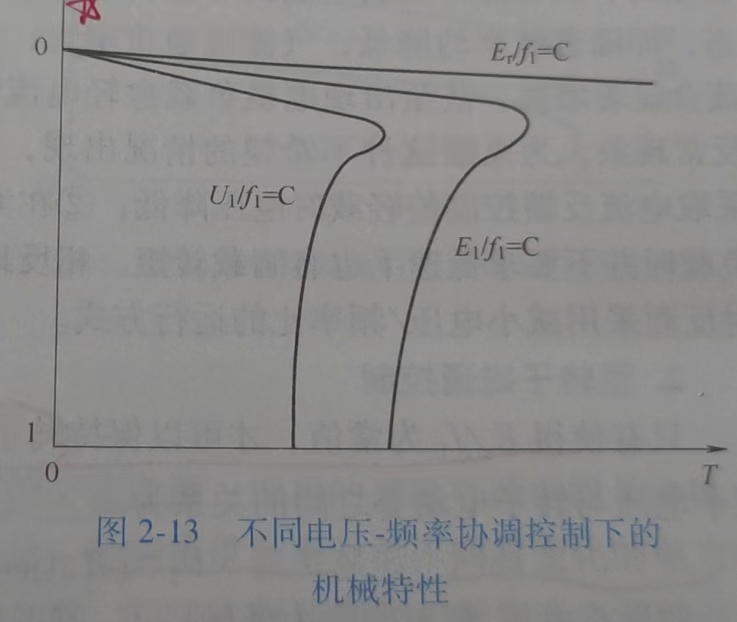
| 恒气隙电势频比 \(E_1/f_1\) | 恒电压频比 \(U_1/f_1\) | 恒转子磁通(转子电势) \(E_r/f_1\) | |
|---|---|---|---|
| 特点 | 气隙磁通 \(\phi_m\) 恒定 需要补偿定子阻抗上的压降 n-T 曲线纯向下平移 低频下 \(T_{st}\) 大,\(I_{st}\) 小 临界转差、转矩更硬,机械特性好 | 类似前一个,但控制更方便 最大转矩 \(T_{st}\) 随频率降低而减小 | 机械特性 n-T 为直线 不同同步速下,为一簇平行线 工作特性好,由高性能电机实现 |
非正弦供电的影响
磁路工作点改变
高次谐波使气隙磁密幅值增加(\(B=B_1+B_5+B_7+\dots>B_1\)),功率因数 \(\cos\varphi\) 下降,磁路计算和空载试验等需要提高设计电压
定子漏抗减小
谐波电流使槽电流增大,槽磁漏增加,饱和程度提高 → 定子漏抗 \(X_{\sigma1}\) 减小
转子集肤效应
高次谐波转差率 \(s_k\approx1\),频率较高,集肤效应强 → 转子电阻增大,转子槽漏抗减小(等效磁链减小) → 增加转子谐波损耗
功率因数下降
电流有效值增大,气隙磁密增大 → 磁路饱和程度提高,无功励磁电流增加 → 功率因数明显下降
损耗与效率
异步电动机损耗增大,效率下降。主要影响来自于转子谐波损耗,与负载关系不大。
谐波转矩的影响
- 恒定谐波转矩:谐波磁场转差率 \(s_k\approx1\),内功率因数角 \(\psi'=\text{atg}\frac{s_kk\omega_1L_2'}{R_2'}\) 较小,基本都是无功电流 → 同次电流产生较小的异步转矩(可忽略)
- 脉动谐波转矩:不同次数的谐波磁场与基波磁场相互作用,产生高频交变的脉动转矩,平均值为0但幅值较大(如5次负序电流和7次正序电流都会产生6倍基频的脉动转矩)
电应力
高瞬间电压变化梯度 \(\frac{\text dv}{\text dt}\) → 浪涌电压尖峰 → 各线圈间电压按分布电容分配 → 约40%电压加在第一个线圈上,易绝缘老化
轴电流
零序电压 \(\frac{U_A+U_B+U_C}3\ne0\),产生流过轴承的电流(高频 → 阻抗小 → 电流大)
可以采用增大气隙、绝缘轴承(即增大阻抗)、经隔离变压器接地等方式消除
- 电压源型非正弦电源输出,选漏抗大的电机(限制谐波电流)
- 电流源型非正弦电源输出,选漏抗小的电机(限制谐波电压)
静止变频器
可以看看这个:电力电子技术 | Paradox's Website (zju-paradox.top)
变频调速实现方法
正弦脉宽调制 SPWM
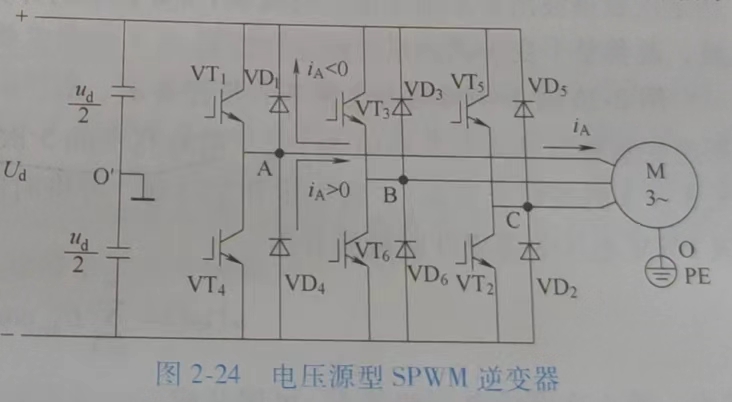
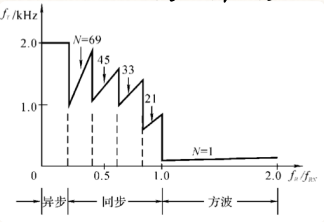
| 单极性控制 | 双极性控制 | 载波比N |
|---|---|---|
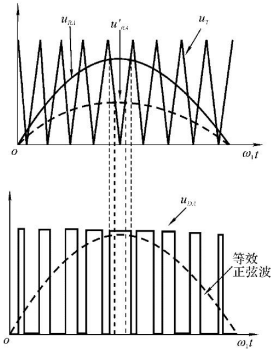 | 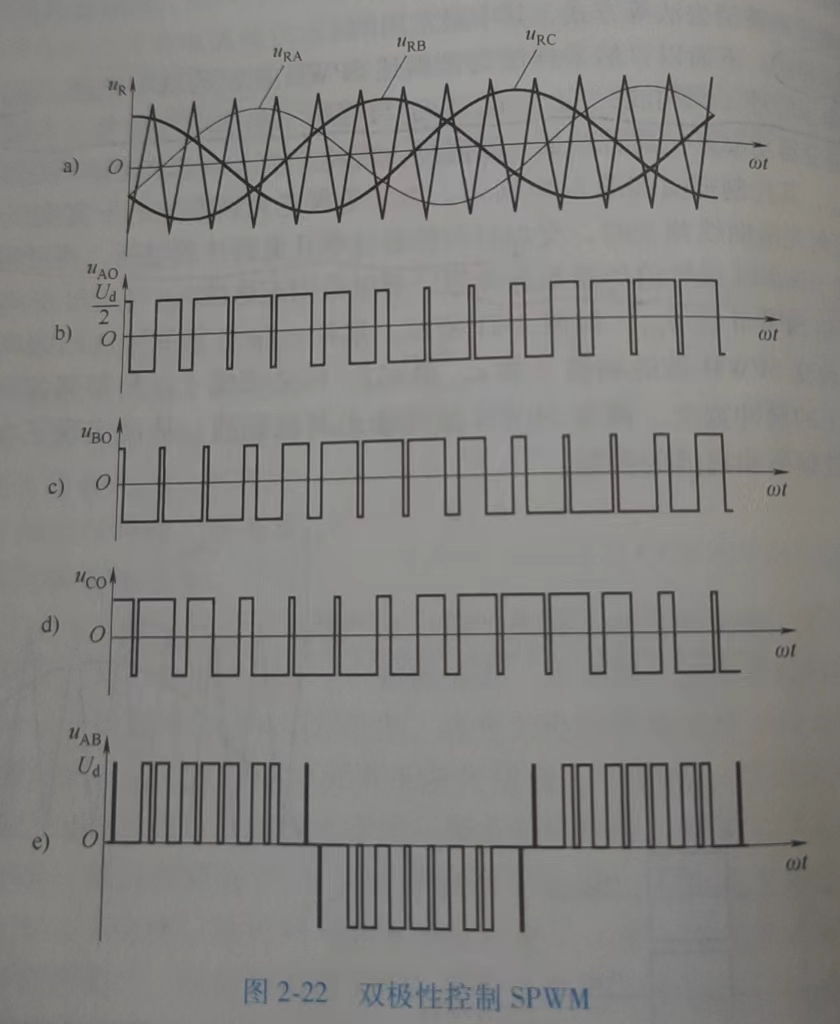 |  |
- 具体实现方法:
- 自然采样法:通过一组三相对称的正弦参考信号(调制波)与等腰三角电压信号(载波)进行比较,由交点处控制通断
- 制定谐波消去法:解方程
- 双极性控制:
- PWM 是 \(\pm\frac{U_d}2\) ,得到输出电压 \(u_R=(2D-1)\frac{U_d}2\)
- 线电压 \(U_{AB}=U_A-U_B\),由 \(\pm U_d,0\) 三种电压选择
- 电压控制:
- 三角波频率(载波频率)→ 开关频率,越高性能越好
- 正弦波频率、幅值 → 输出正弦波频率、幅值
- 载波比 \(N=f_T/f_R\):
- 最好选择 N 为 3 的倍数,这样能保证输出波形正负半波对称,且三相波形互差120°对称
- 开关死区的影响:
- 由于开关死区,会存在上下两管均关断的情况,因此输出电压幅值下降。平均偏差电压 \(U_{ef}=\frac{t_dU_dN}T\)
- 变频器输出频率越低,死区影响越严重。
- 功率因数越大,电压电流同向越久,死区影响越严重。
电流跟踪控制
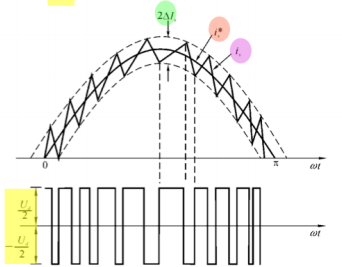
实际上就是一个很简单的滞环控制,以输出接近正弦的定子三相电流为目的。优点是简单,缺点是难以进行频域分析(PWM无规律,不确定)
磁链跟踪控制 SVPWM
基本理论
最终目的是产生圆形的旋转磁场,从而产生恒定的电磁转矩。磁链的改变依靠电压空间矢量作用获得,因此称为电压空间矢量调整 SVPWM。
可以参考电机建模里的这个:电机系统建模与分析 | Paradox's Website (zju-paradox.top),但是电机建模里面是恒幅值变换,这里是恒功率变换,需要把系数 \(\frac23\) 换成 \(\sqrt{\frac23}\)。
\[ u_s=\sqrt{\frac23}U_m(\cos\omega_1t+\cos(\omega_1t-\frac23\pi)+\cos(\omega_1t+\frac23\pi))=\sqrt{\frac23}U_me^{j\omega_1t} \]
电压和磁链的关系式由 \(u_s=R_si_s+\text p\psi_s\) 导出,忽略定子电阻的压降,则有:
\[ u_s=\frac{\text d\psi_s}{\text dt}~;~\Delta\psi_s=u_s\cdot\Delta t \]
如果电压通过电压源型逆变器供电,那么每相定子电压有 \(\pm\frac{U_d}2\) 两种状态,分别用 \(1,0\) 表示。那么三相定子电压就可以用一组向量 \(s_{ABC}=(s_A,s_B,s_C)\) 表示,一共 \(2^3=8\) 种可能。其中 \(s_{ABC}=(1,1,1)=(0,0,0)\),所表现出的定子电压综合矢量都是 \(u_s=0\),剩下6种在空间内均匀分布(间隔60°)。
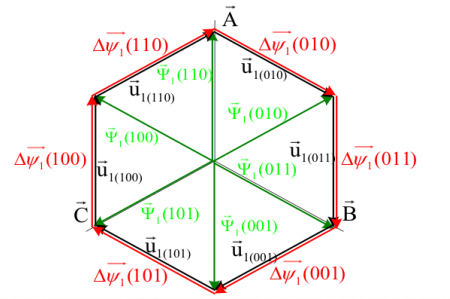
正六边形旋转磁场
如上图所示,令6个有效电压矢量在一个周期内按顺序工作 \(\frac{\pi}3\) 电角度,即 \(\Delta t=\frac{\pi}{3\omega_1}\)。这样的话磁链就会沿着上图那样的六边形进行旋转,磁链幅值为:
\[ |\psi_s(k)|=|\Delta\psi_s(k)|=\sqrt{\frac23}\frac{\pi}{3\omega_1}U_d \]
如“变频调速理论基础”中所说,基频下调时需要维持气隙磁通恒定,但是随着频率 \(\Omega_1\) 的减小,定子磁链会上升,这时候就要插入零电压矢量 \(u_0\) 或 \(u_7\)。有效电压矢量只工作 \(\Delta t_1=\frac{\pi}{3\omega_n}<\Delta t\) 的时间,剩下的时间 \(\Delta t_0=\Delta t-\Delta t_1\) 用零电压矢量来补。具体用 \(u_0\) 还是 \(u_7\) 考虑当前电压矢量变到哪个比较方便。
\[ |\psi_s(k)|=|\Delta\psi_s(k)|=|u_s(k)\Delta t_1+0\Delta t_0 |=\sqrt{\frac23}U_d\Delta t_1 \]
基频以上本来就是弱磁控制,根据公式磁链减小,因此没关系。
期望电压空间矢量的合成
通过对空间矢量的细分与组合,可以实现更接近圆形的正多边形。先读取当前定子磁链 \(\vec{\psi_s}\),判断所需的定子电压矢量 \(\vec{u_s}\)。然后根据该电压矢量所处的位置,用临近的两个有效电压矢量和零电压矢量(若需)进行合成如下:

\[ \vec{u_s}=\frac{t_1}{T_0}\vec{u_1}+\frac{t_2}{T_0}\vec{u_2}+\frac{t_0}{T_0}\vec{u_0} \]
其中 \(T_0\) 是开关周期,个人感觉应该是“想细分的正多边形边数”\(n=\frac T{T_0}=\frac{2\pi}{\omega_1T_0}\)
变频调速系统
开环调速系统
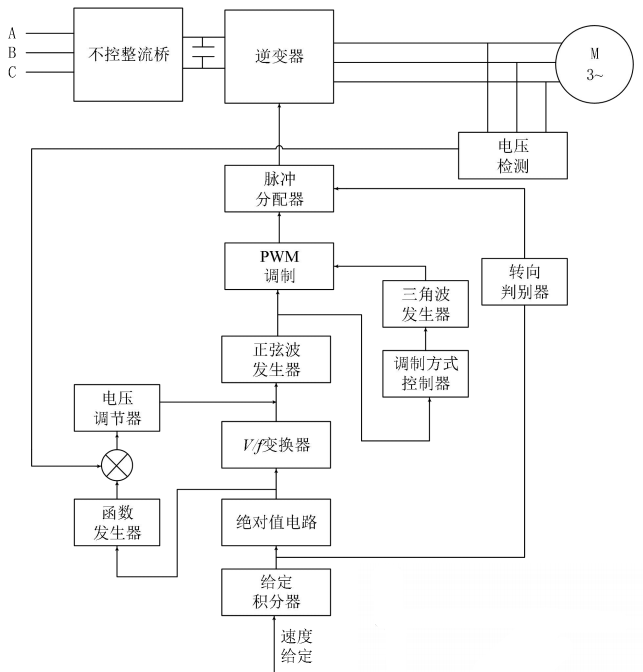
- 输入的速度给定通过变换得到所需的电机运行频率,以电压 V 的形式呈现:
- 一方面,频率给定经 V/f 变换器(从 V 到 f )产生了决定正弦调制波频率的脉冲,来控制正弦调制波 \(u_R\) 的频率
- 另一方面,频率给定经函数发生器实现了对正弦调制波幅值的控制,即基频以下电压降低,保证气隙磁通恒定,最大转矩恒定;基频以上电压恒定,功率恒定
- 至此,正弦波发生器产生频率和幅值都与速度指令相适应的正弦调制波
- 一方面,调制波通过调制方式控制器决定三角波载波的频率
- 另一方面,正弦调制波与三角波载波作用,产生用于控制逆变器的 PWM
- 特点:
- 无频率反馈,有电压反馈
- 频率给定后不变,电机转速会随着负载增大而变小。适合长期稳态运行,调速精度不高的场合
闭环调速系统
控制原理
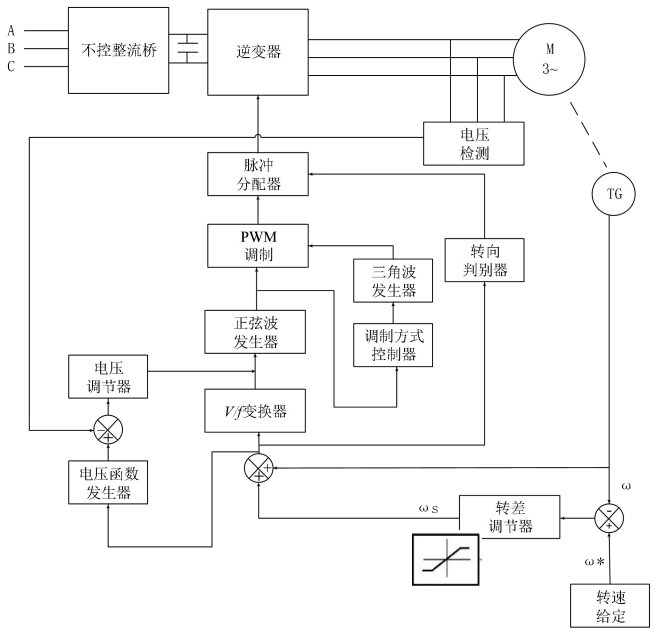
控制原理与方法:
\[ T_e=C_t\phi_mI_2'\cos\psi_2\approx C_t\phi_mI_2'\approx C_t'\phi_m^2\omega_s \]也就是说在气隙磁通不变的情况下,电磁转矩与转差频率成正比。除了上文函数发生器之外,可以参考书本 p64 的方法来实现更加精确的气隙磁通恒定。
开环调速系统可以实现同步速 \(\omega_1\) 的控制,因此闭环的关键就是实现对转速和同步速的闭环:
\[ \omega_1(用于调节同步速)=\omega(现在的)+\omega_s(所需的) \]
控制框图的另一种画法:
控制过程
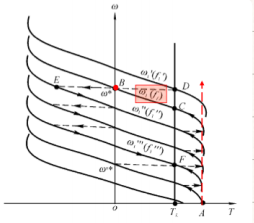
- 起动时 \(n=0\),\(\omega^*-\omega\) 很大,因此输出 \(T_{em}=T_{m}\),转速沿着最大转矩的铅垂线直线上升
- 直到 \(\omega\) 接近 \(\omega^*\),电磁转矩逐渐减小,逐渐稳定到机械特性与负载转矩的交点
- 当给定转速突然减小,电机工作点将从D点移到E点,电磁转矩 \(T_{em}=-T_{m}\),在接近给定转速时再沿着机械特性(?)下降
高性能控制
矢量控制
异步电机数学模型
坐标变换仍然可以参考电机建模:电机系统建模与分析 | Paradox's Website (zju-paradox.top),但是电机建模里面是恒幅值变换(前面有一章是恒功率变化,那里需要把系数 \(\frac23\) 换成 \(\sqrt{\frac23}\))。关于 \((\alpha-\beta-0)\) 到 \((d-q-0)\) 的坐标变换方式在文章里已经写的很明白了,这里不再赘述。
- M轴(d)为转子磁链矢量(转子磁场)的方向,T轴(q)与之垂直。
- 为将异步电机等效为直流电机,必须采用恒转子电动势频比(\(\frac{E_r}f=C\))控制
- 仍然满足:
- 旋转电势、转矩、转子电流落在交轴上:\(i_{rM}=0\)(稳态运行时)
- 励磁磁链落在直轴上:\(\psi_{rT}=0\)
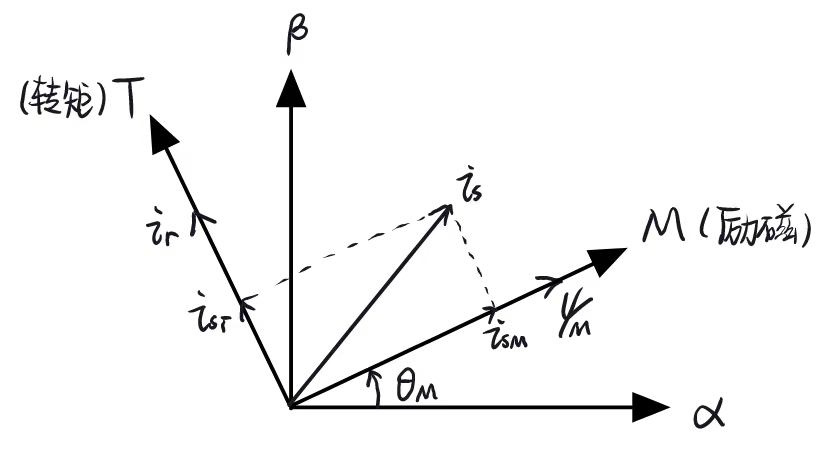
异步电机物理模型
异步电机电感矩阵为 \(L=\begin{bmatrix}L_{SS}&L_{SR}\\L_{RS}&L_{RR} \end{bmatrix}_{6\times6}\),其中:
- 各相自感:\(L_{mm}+L_{s\sigma}\) 或 \(L_{mm}+L_{r\sigma}\)
- 同相间互感(如Aa):\(L_{mm}\)
- 异相间互感(如AB):\(-\frac12L_{mm}\)
定子磁链:
\[ \psi_{s}=L_si_s+L_mi_r~~(L_m=\frac32L_{mm},L_s=L_m+L_{s\sigma}) \]转子磁链:
\[ \psi_{r}=L_si_s+L_ri_r~~(L_r=L_m+L_{r\sigma}) \]- 定转子磁链都可以往两个轴(M、T)上分解,只需要给电流对应加下标就行。
电压方程:\(u_s=R_si_s+\text p\psi_s+j\omega_1\psi_s~,~u_r=R_ti_r+\text p\psi_r+j\omega_s\psi_r\)
电磁转矩:
\[ T_e=\frac 32p\frac{L_m}{L_r}\psi_{rM}i_{sT}~~(p是极对数,书上写错了) \]
当转子磁链的幅值 \(\psi_{rM}\) 保持不变的时候,通过调节定子电流的转矩分量 \(i_{sT}\) 即可控制电磁转矩。定子电流:
\[ i_{sT}=\frac{\omega_s\psi_{rM}\tau_r}{L_m}~~(\tau_r=\frac{L_r}{R_r}) \]转子磁链:
\[ \psi_r=\psi_{rM}=\frac{L_m}{1+\tau_rp}i_{sM} \]- 定子电流的直轴(M轴)分量控制转子磁链,定子电流的交轴(T轴)分量控制电磁转矩,实现解耦
转差频率:
\[ \omega_s=\frac{L_mi_{sT}^*}{\tau_r\psi_r^*}=\frac{\tau_rp+1}{\tau_r}\frac{i_{sT}}{i_{sM}} \]
转子磁场定向技术
| 磁通检测—电压模型 | 磁通检测—电流模型 | 转差频率控制式 | |
|---|---|---|---|
| 输入 | 定子电压 \(u_{s\alpha\beta}\)、定子电流 \(i_{s\alpha\beta}\) | 定子电流 \(i_{s\alpha\beta}\)、电机转速 \(\omega_r\) | \(i_{sT}^*,\psi_{r^*},\omega\) |
| 过程 | \(\begin{gather*}\psi_{r\alpha}=\frac{L_r}{L_mp}[u_{s\alpha}-(R_s+\sigma L_sp)i_{s\alpha}]\\\psi_{r\beta}=\frac{L_r}{L_mp}[u_{s\beta}-(R_s+\sigma L_sp)i_{s\beta}] \end{gather*}\) | \(\begin{gather*}\psi_{r\alpha}=\frac{1}{\tau_rp}[L_mi_{s\alpha}-\omega \tau_r\psi_{r\beta}]\\\psi_{r\beta}=\frac{1}{\tau_rp}[L_mi_{s\beta}+\omega \tau_r\psi_{r\alpha}] \end{gather*}\) | \(\begin{gather*} \omega_s=\frac{L_mi_{sT}^*}{\tau_r\psi_r^*}\\=\frac{\tau_rp+1}{\tau_r}\frac{i_{sT}}{i_{sM}}\end{gather*}\) |
| 输出 | \(\begin{gather*}\psi_r=\sqrt{\psi_{r\alpha}^2+\psi_{r\beta}^2}\\\theta_M=\text{atg}(\psi_{r\beta}/\psi_{r\alpha}) \end{gather*}\) | \(\begin{gather*}\psi_r=\sqrt{\psi_{r\alpha}^2+\psi_{r\beta}^2}\\\theta_M=\text{atg}(\psi_{r\beta}/\psi_{r\alpha}) \end{gather*}\) | \(\theta_M=\int(\omega_s+\omega)\text dt\) |
控制系统实例
- Te是带 1.5 这个系数的,下面写错了,他书里也有点问题
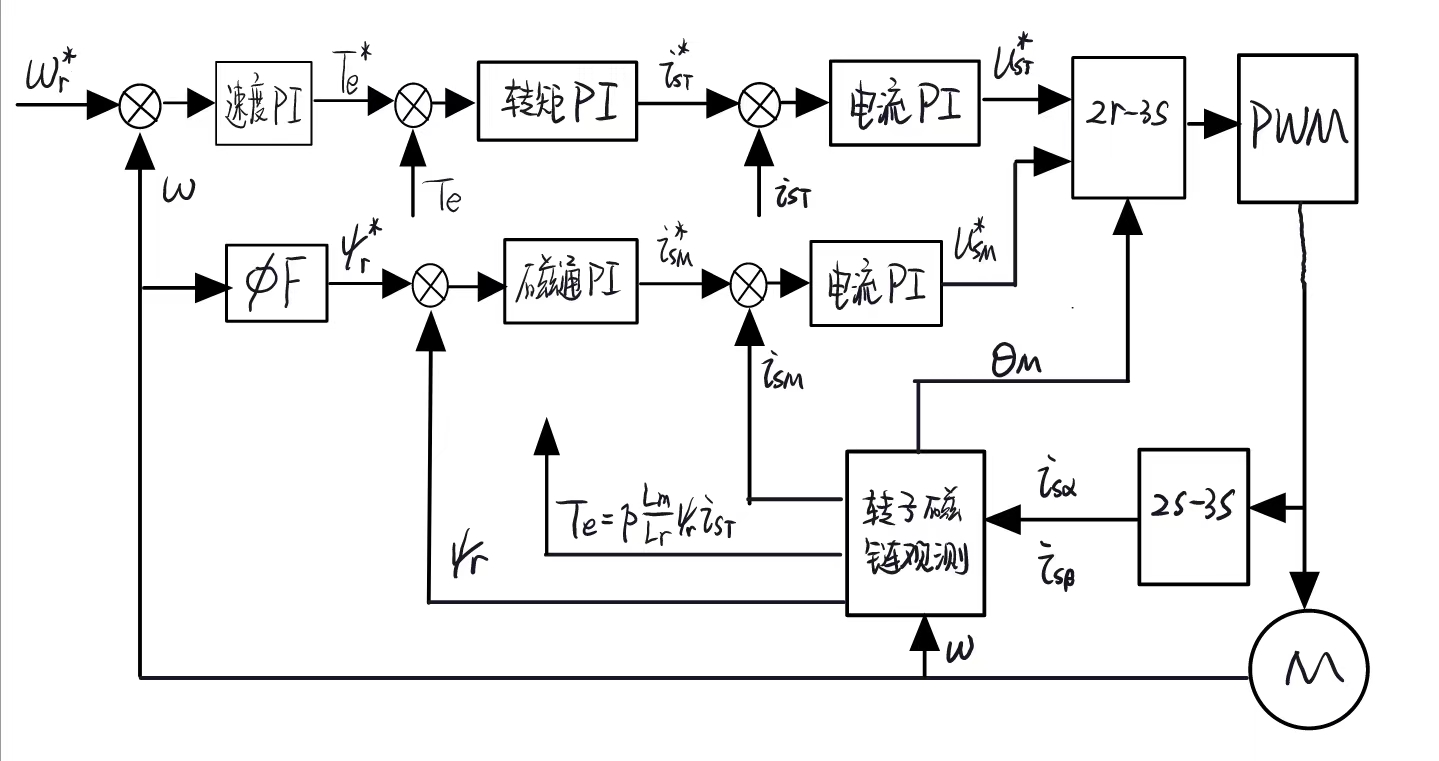
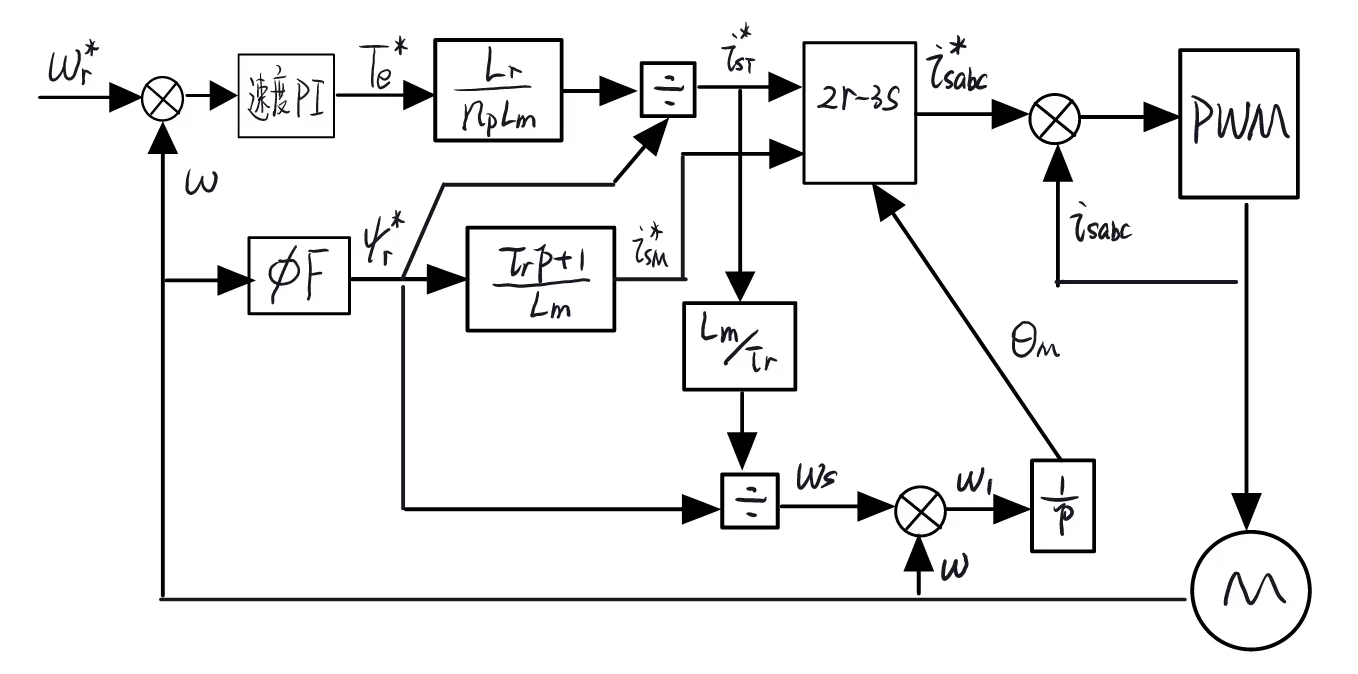
以下是控制框图的注意事项:
控制框图可以拆分为:物理模型前向通道 + 反馈回路(转子磁场观测)+ 输出
物理模型所述的前向通道:
如上文所述,定子电流的直轴(M轴)分量控制转子磁链,定子电流的交轴(T轴)分量控制电磁转矩
这个是电机自带的传递函数,控制框图相当于是逆过程,所以:
- 通过电磁转矩 \(T_e^*\) 得到定子电流交轴分量 \(i_{sT^*}\)
- 通过转子磁链 \(\psi_{r}^*\) 得到定子电流直轴分量 \(i_{sM}^*\)
至于如何得到,方式可以有很多,比如:
- 通过PI控制器等 ST 进行输出,需要引入观测量如 \(T_e\) 等,如图1
- 通过物理模型直接计算,如图2
反馈回路(转子磁场观测):
观测模型主要注意两点:
- 前向通道中是否需要转子磁通 \(\psi_r\),若要,则用磁通检测式,如图1;若不要,可用转差频率定向,如图2
- 这种观测模型的输入是什么?定子电流、转子磁链?
输出:
输出决定了电源的特性,与控制回路关系不大。前向通道所得到的一定是定子电流的M和T轴分量的给定值 \(i_{sM}^*,i_{sT}^*\),可以采取如下措施:
- 直接做电流环控制,得到所需的定子电压给定值
- 对电流直接进行变换,利用变频控制中说的电流跟踪滞环控制进行控制
不需要记具体公式(应该吧),可以用常数、简写等代替。
直接转矩控制
- 直接转矩控制将电机和逆变器作为一个整体来考虑,采用电压空间矢量对定子三相电压作综合描述,在定子坐标系中直接控制定子磁链 \(\psi_s\) 和电磁转矩 \(T_e\)。
数学模型
\[ T_e=\text p\vec \psi_s\times\vec i_s=\text p\frac{L_m}{L_s'L_r}\vec\psi_s\times\vec\psi_r=\text p\frac{L_m}{L_s'L_r}\psi_s\cdot\psi_r\sin\theta_{sr} \]
- 近似认为 \(\psi_r\) 在匀速旋转(速度为同步速,但是这种直接对磁链进行的控制是可以人为控制频率 \(f\) 的),利用 \(\Delta\vec\psi_s=\vec u_s\Delta t\) 来控制定子磁链,进而调节 \(\theta_{sr}\),从而调节电磁转矩。
磁链与转矩观测器
| 电压模型定子磁链观测 | 电流模型定子磁链观测 | 转矩观测 | |
|---|---|---|---|
| 输入 | \(u_{s\alpha},u_{s\beta},i_{s\alpha},i_{s\beta}\) | \(i_{s\alpha},i_{s\beta},\omega_r\) | \(i_{s\alpha},i_{s\beta},\psi_{\alpha},\psi_{\beta}\) |
| 输出 | \(\psi_{s\alpha},\psi_{s\beta}\) 即 $ s,{s}$ | \(\psi_{s\alpha},\psi_{s\beta}\) 即 $s,{s} $ | \(T_e\) |
六边形磁链轨迹控制系统
- 他预先设立了一个换向逻辑,即:
- 采用六边形磁链轨迹控制的时候,某相(abc)磁链的轨迹是一个梯形波
- 通过滞环控制,将这个梯形波等效成方波(即1和0),方波周期为磁链轨迹周期
- 根据磁链和电压图,六种磁链向量(如 \(\psi_{abc}=101\))会分别对应六种电压向量(如 \(u_{abc}=011\))
- 把第三步的这个对应关系做成一个换向逻辑,控制三相电压开关
- 这个只能控制相位,磁链幅值需要通过电磁转矩滞环控制,来作为上面电压开关的总开关
- 所以他的控制系统长这样:
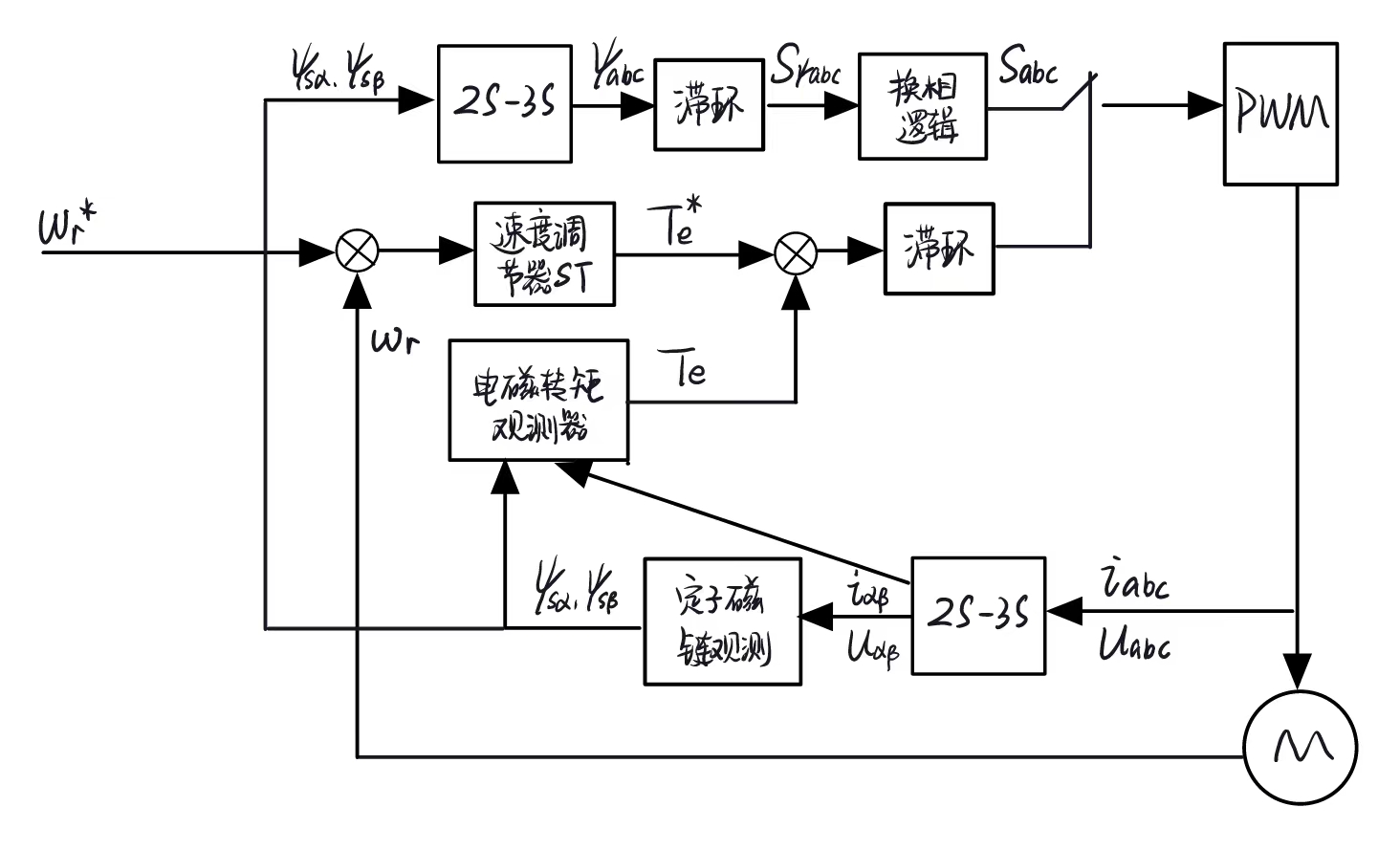
变压变频控制 VVVF
- 变频调速控制主要通过零电压矢量时间 \(t_0\) 和控制有效电压矢量时间 \(t_1,t_2\) 来实现
- 基频以下,恒磁通控制:频率 \(f\) 降低,周期 \(T\) 上升;\(t_1,t_2\) 不变令 \(t_0\) 增大,使电压、磁通不变
- 基频以上,弱磁控制:频率 \(f\) 提高,周期 \(T\) 减小;令\(t_1,t_2\) 减小满足频率变化,相应的电压、磁通要减少
- 在基频时,\(t_0=0\)。
绕线式异步电机控制
- 这里主要讲的是变转差调速,即通过调节转差功率 \(P_{s}=sP_{em}\) 来调节转差频率,进而调节转速。
- 但是如果在转子上接入电动势,那么转差功率将会被附加电动势吸收转化,回馈电网
串级调速
- 在转子回路中传入一个与转子同频率 \(sf_1\) 的附加电动势 \(E_f\),取代转子电阻 \(R_f\)。
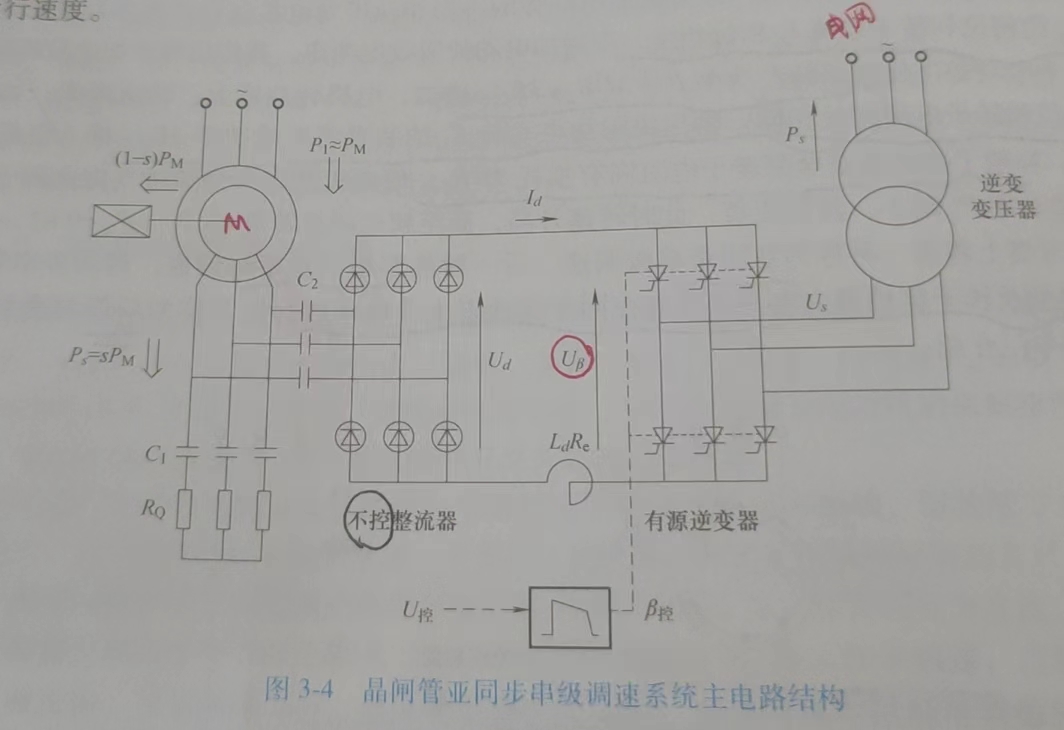
| \(E_f\) | 假设 | \(P_s\) | 转速 | 能量 | |
|---|---|---|---|---|---|
| 亚同步 | \(E_f\)与\(I_2\)反相位 | \(E_f\)↑ | \(P_s=sP_{em}=3I_2^2R_2+3E_fI_2\) | 下降↓ | \(P_s\)从电机流向电网 |
| 超同步 | \(E_f\)与\(I_2\)同相位 | \(E_f\)↑ | \(P_s=sP_{em}=3I_2^2R_2-3E_fI_2\) | 上升↑ | \(P_s\)从电网流向电机 |
亚同步
- 机械特性与电压关系式
\[ \begin{gather*} sE_{d0}-\Delta U_M=U_d=U_{\beta}+R_eI_d=E_{\beta}+\Delta U_s+R_eI_d\\ \Rightarrow s=K_1\cos\beta+K_2I_d\\n=n_1(1-s)=n_1(1-K_1\cos\beta-K_2I_d) \end{gather*} \]
结论:通过改变逆变角 \(\beta\) 进行调速,但是转速会随着负载电流的上升而下降,特性较软
功率因数问题
逆变器晶闸管换向需要落后的无功,异步电动机也要落后无功,因此功率因数会比较低
可以看到下面这幅图(亚同步)里面一部分功率 \(P_B\) 经过晶闸管之后逆变回到电网,与上面这个表格是符合的
说过附加电动势 \(E_f\) 的频率是转子同频,所以频率很低,这个时候不控整流期间就会有严重的换向重叠现象,因此功率因数进一步减小
\[ \cos\varphi=\frac{P_1-P_{\beta}}{\sqrt{(P_1-P_{\beta})^2+(Q_1+Q_{\beta})^2}} \]
\[ \cos\varphi_D=\frac{P_1}{P_1^2+Q_1^2} \]
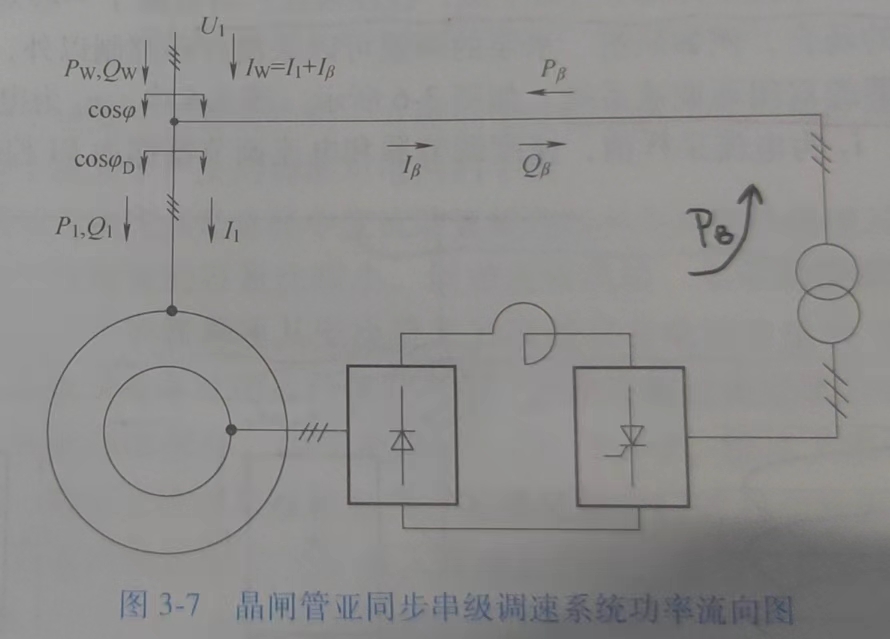
超同步 - 双馈调速与四象限运行
亚同步里面转子侧用的不控整流,在双馈调速系统(超同步)里面用的可控整流,这样能量才能从电网流向电机(即从右往左流动)
值得注意的是两个整流桥是反向连接,并且工作状态是互补的(即一个整流另一个逆变)
通过对整流桥电压正负与工作状态的调节,可以实现四象限运行,这四种状态由 2种电压(正负)× 2组状态(整流逆变/逆变整流)构成。可以实现 2种转速(亚/超同步)× 2种能量流动(电动/发电) 这四种状态。
双馈调速系统主要通过对整流桥从不控变成可控的改进,能减小装置容量一半,提高功率因数,实现四象限运行。
同步电机控制
电励磁
方程式
同步电机的方程看这里:电机学笔记(总) | Paradox's Website (zju-paradox.top),前面那个叫励磁转矩,后面那个叫同步磁阻转矩。把其他公式带进来,得到电磁转矩如下(前面是电励磁,后面是永磁):
\[ T_e= p~\left[M_fi_fi_q+(L_d-L_q)i_di_q+(M_Di_Di_q-M_Qi_Qi_d) \right] \]
\[ T_e=p~(\psi_fi_q+(L_d-L_q)i_di_q) \]
\[ T_e=p~\psi_mi_{sT} \]
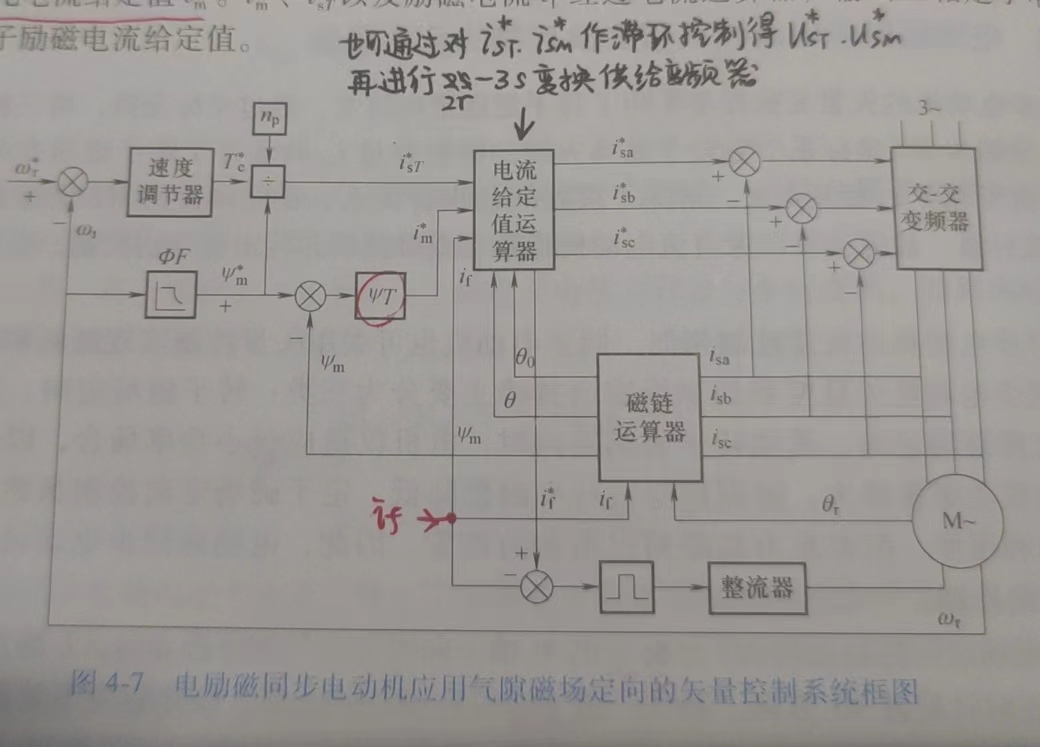
通过励磁磁化电流 \(i_m\) 使气隙磁链 \(\psi_m\) 保持不变,这样通过调节定子电流的转矩 T 分量 \(i_{sT}\) 来控制电磁转矩
观测器
| 磁链 | 电流给定值 | |
|---|---|---|
| 输入 | \(i_d,i_q,i_f\) | \(\theta,\theta_0,i_f,i_m^*,i_{sT}^*\) |
| 输出 | \(\psi_m,\theta,\theta_0\) | \(i_f^*,i_{abc}\) |
| 备注 | \(i_{dq}\)需要\(\theta_r\)来进行3s-2r | \(i_m\)和\(i_{sT}\)控制\(T_e\),因此需要控制 |
| 比正常系统多一个 \(i_f\) 的输入 |
- 这个空间矢量图比较复杂,需要解释一下:
- 这里有两个运动两相坐标系,一个是直轴-交轴坐标系 \(d-q\),一个是磁链-转矩坐标系 \(M-T\)
- 有两个电流,定子电流 \(i_s\) 可以在 M-T 分解为 \(i_{sM},i_{sT}\),转子电流就是励磁电流 \(i_f\),因为是直轴励磁,因此 \(i_f\) 落在 d 轴上
- 角度也有两个,其中 d 轴与 a 相的夹角为 \(\theta_r\),M 轴与 a 相的夹角为 \(\theta_0\),这两个轴之间的夹角为 \(\theta\),其中 M 轴要超前 d 轴一点。有:\(\theta_r+\theta=\theta_0\)
- 磁化电流 \(i_m\) 并不是实际存在的电流,仅是定转子电流在 M 轴(转子磁链轴)上的投影,即:\(i_m=i_{sM}+i_f\cos\theta_0\)
- \(\theta_r\) 电机是可以直接输出的,\(\psi_f\) 或者 \(i_f\) 也是可以有外部可以测量直接输入的
永磁电机
- 贴片永磁的特点是直轴和交轴电感一样,即 \(L_d=L_q\),所以电磁转矩为 \(T_e=p\,\psi_fi_q\)
- 还有其他永磁电机,\(L_d\ne L_q\)
- 没有转子电流,但是直轴会多一个磁链 \(\psi_f\)
| 基于 \(i_d=0\) 的控制 | 最大转矩电流比 MTPA 控制 | |
|---|---|---|
| \(T_e\) | \(T_e=p~\psi_fi_q\) | \(T_e^*=i_q^*(1-i_d^*)\)(*是标幺值) |
| 图解 | 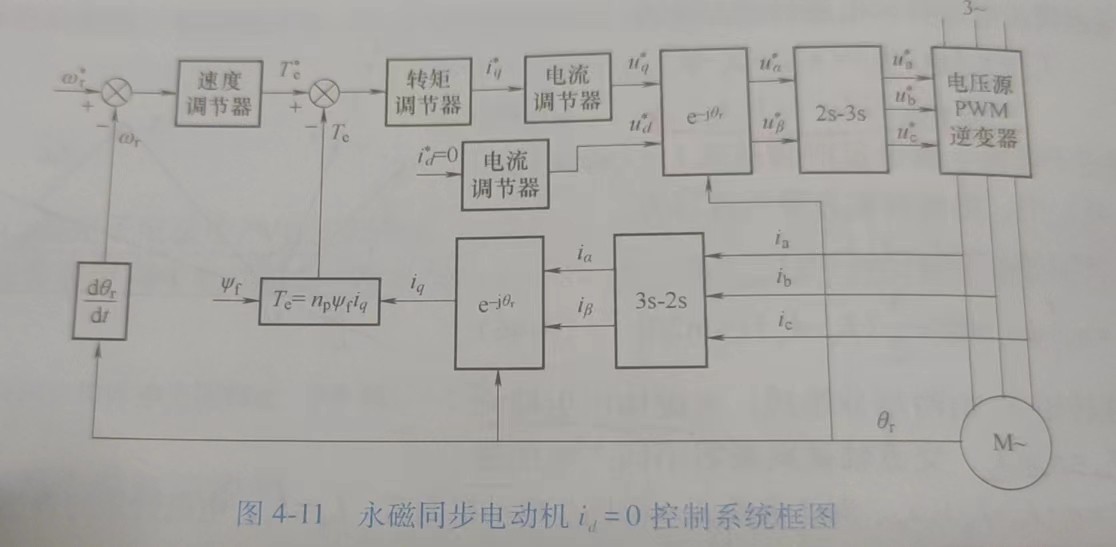 | 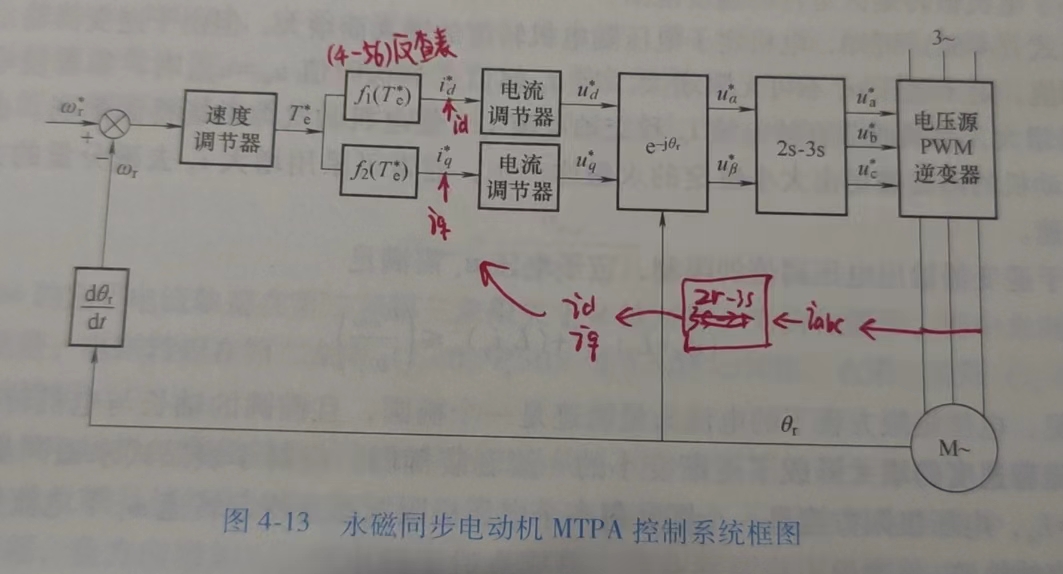 |
| 注释 | 控制极其简单!因为励磁 \(\psi_f\) 固定,所以只用控制交轴电流 $i_q $ 即可完成转矩控制。为了定子电流最小,可以直接让 \(i_d^*=0\) | 控制也很简单,主要思想是在给定转矩下得到最小可用的定子电流 |
P.S
- 所有电机的输入都长这个样子(或者再多加一点):
- 最终得到的控制量一定是两相电流参考值,要么是 \(i_{sM}^*+i_{sT}^*\),要么是 \(i_d^*+i_q^*\)
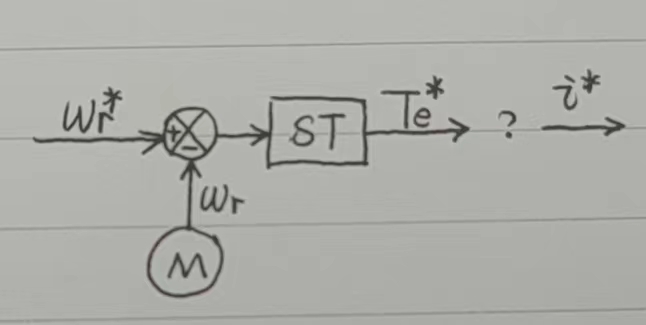
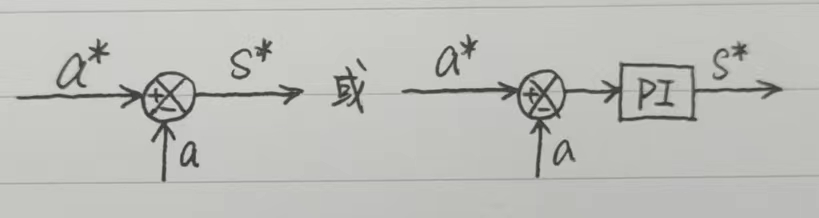
- 我们经常见到下面这幅图的小模块,他的意思是:输出 s 能控制输入 a,比如转矩控制转速,电流控制转矩,电流控制磁链,电压控制电流